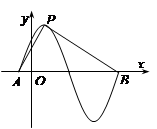题目内容
已知函数f(x)=cos2(x-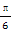 )-sin2x.
)-sin2x.
(1)求f(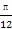 )的值.
)的值.
(2)若对于任意的x∈[0,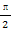 ],都有f(x)≤c,求实数c的取值范围.
],都有f(x)≤c,求实数c的取值范围.
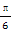 )-sin2x.
)-sin2x.(1)求f(
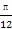 )的值.
)的值.(2)若对于任意的x∈[0,
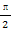 ],都有f(x)≤c,求实数c的取值范围.
],都有f(x)≤c,求实数c的取值范围.(1)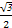 (2) [
(2) [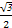 ,+∞)
,+∞)
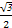 (2) [
(2) [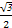 ,+∞)
,+∞)(1)f(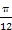 )=cos2(-
)=cos2(-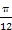 )-sin2
)-sin2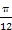 =cos
=cos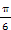 =
=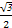 .
.
(2)f(x)= [1+cos(2x-
[1+cos(2x-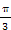 )]-
)]- (1-cos2x)
(1-cos2x)
= [cos(2x-
[cos(2x-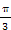 )+cos2x]
)+cos2x]
= (
(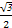 sin2x+
sin2x+ cos2x)
cos2x)
=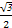 sin(2x+
sin(2x+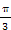 ).
).
因为x∈[0,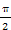 ],所以2x+
],所以2x+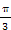 ∈[
∈[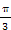 ,
,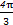 ],
],
所以当2x+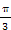 =
=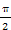 ,即x=
,即x=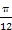 时,f(x)取得最大值
时,f(x)取得最大值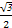 .
.
所以对于任意的x∈[0,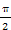 ],f(x)≤c等价于
],f(x)≤c等价于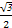 ≤c.
≤c.
故对于任意的x∈[0,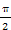 ],都有f(x)≤c时,c的取值范围是[
],都有f(x)≤c时,c的取值范围是[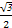 ,+∞).
,+∞).
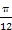 )=cos2(-
)=cos2(-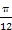 )-sin2
)-sin2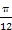 =cos
=cos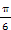 =
=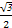 .
.(2)f(x)=
 [1+cos(2x-
[1+cos(2x-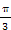 )]-
)]- (1-cos2x)
(1-cos2x)=
 [cos(2x-
[cos(2x-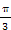 )+cos2x]
)+cos2x]=
 (
(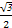 sin2x+
sin2x+ cos2x)
cos2x)=
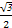 sin(2x+
sin(2x+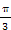 ).
).因为x∈[0,
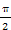 ],所以2x+
],所以2x+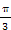 ∈[
∈[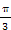 ,
,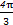 ],
],所以当2x+
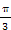 =
=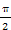 ,即x=
,即x=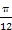 时,f(x)取得最大值
时,f(x)取得最大值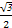 .
.所以对于任意的x∈[0,
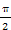 ],f(x)≤c等价于
],f(x)≤c等价于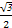 ≤c.
≤c.故对于任意的x∈[0,
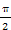 ],都有f(x)≤c时,c的取值范围是[
],都有f(x)≤c时,c的取值范围是[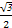 ,+∞).
,+∞).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
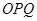 是半径为1,圆心角为
是半径为1,圆心角为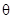 的扇形,
的扇形,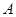 是扇形弧
是扇形弧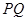 上的动点,
上的动点,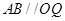 ,
,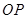 与
与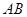 交于点
交于点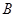 ,
,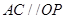 ,
,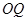 与
与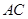 交于点
交于点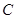 .记
.记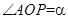 .
.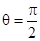 ,如图3,当角
,如图3,当角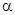 取何值时,能使矩形
取何值时,能使矩形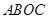 的面积最大;
的面积最大;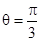 ,如图4,当角
,如图4,当角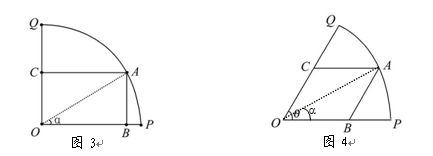
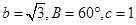 ;(2)
;(2)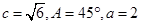 .
.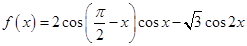 ,
,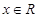 .
. 的值;
的值;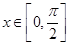 时,求
时,求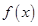 的最值.
的最值.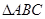 中,
中,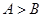 是
是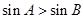 成立的充要条件;
成立的充要条件; 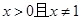 时,有
时,有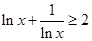 ;
;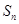 是等差数列
是等差数列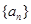 的前n项和,若
的前n项和,若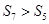 ,则
,则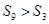 ;
;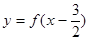 为R上的奇函数,则函数
为R上的奇函数,则函数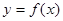 的图象一定关于点
的图象一定关于点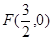 成中心对称.
成中心对称.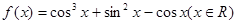 有最大值为
有最大值为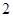 ,有最小值为0。
,有最小值为0。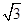 sin 3x+cos 3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
sin 3x+cos 3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.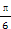 ),1),b=(4,4cosα-
),1),b=(4,4cosα-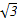 ),若a⊥b,则sin(α+
),若a⊥b,则sin(α+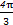 )=( )
)=( )

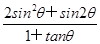 =k,0<θ<
=k,0<θ<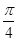 ,则sinθ-
,则sinθ-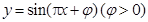 的部分图象如右图所示,设
的部分图象如右图所示,设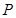 是图象的最高点,
是图象的最高点,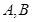 是图象与
是图象与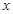 轴的交点,则
轴的交点,则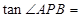 ( )
( )