题目内容
【题目】已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b. 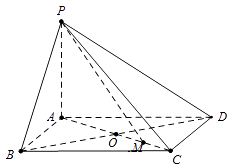
(1)求证:平面PBD⊥平面PAC;
(2)设AC与BD交于点O,M为OC中点,若二面角O﹣PM﹣D的正切值为2 ![]() ,求a:b的值.
,求a:b的值.
【答案】
(1)证明:因为PA⊥平面ABCD,所以PA⊥BD,
又ABCD为菱形,所以AC⊥BD,
因为PA∩AC=A,所以BD⊥平面PAC,
因为BD平面PBD,所以平面PBD⊥平面PAC.
(2)解:过O作OH⊥PM交PM于H,连HD,
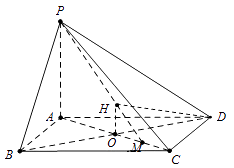
因为DO⊥平面PAC,由三垂线定理可得DH⊥PM,所以∠OHD为A﹣PM﹣D的平面角
又 ![]() ,且
,且 ![]()
从而 ![]()
∴ ![]()
所以9a2=16b2,即 ![]()
【解析】(1)根据线面垂直的判定,证明BD⊥平面PAC,利用面面垂直的判定,证明平面PBD⊥平面PAC.(2)过O作OH⊥PM交PM于H,连HD,则∠OHD为A﹣PM﹣D的平面角,利用二面角O﹣PM﹣D的正切值为2 ![]() ,即可求a:b的值.
,即可求a:b的值.

 阳光课堂课时作业系列答案
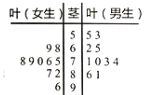
阳光课堂课时作业系列答案【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.如图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”. 
(1)求m,n的值,并求这100名学生月消费金额的样本平均数 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |