题目内容
某同学设计一个摸奖游戏:箱内有红球3个,白球4个,黑球5个.每次任取一个,有放回地抽取3次为一次摸奖.至少有两个红球为一等奖,记2分;红、白、黑球各一个为二等奖,记1分;否则没有奖,记0分.
(I)求一次摸奖中一等奖的概率;
(II)求一次摸奖得分的分布列和期望.
解:(I)每次有放回地抽取,取到红球的概率为 ;取到白球的概率为
;取到白球的概率为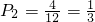 ;取到
;取到
黑球的概率为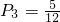 ;
;
一次摸奖中一等奖的概率为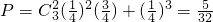 .
.
(II)设ξ表示一次摸奖的得分,则ξ可能的取值为0,1,2. ;
;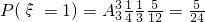 ;
;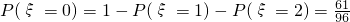 ∴一次摸奖得分ξ的分布列为
∴一次摸奖得分ξ的分布列为
期望为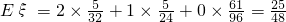 .
.
分析:(I)每次有放回地抽取,取到红球的概率为 ;取到白球的概率为
;取到白球的概率为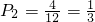 ;取到黑球的概率为
;取到黑球的概率为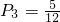 ;由此能求出一次摸奖中一等奖的概率.
;由此能求出一次摸奖中一等奖的概率.
(II)设ξ表示一次摸奖的得分,则ξ可能的取值为0,1,2. ;
;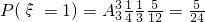 ;由此能求出一次摸奖得分ξ的分布列和期望.
;由此能求出一次摸奖得分ξ的分布列和期望.
点评:本题考查n次独立重复试验恰好发生k次的概率,解题时要注意离散型随机变量ξ的分布列和期望的求法.
 ;取到白球的概率为
;取到白球的概率为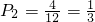 ;取到
;取到黑球的概率为
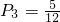 ;
;一次摸奖中一等奖的概率为
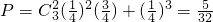 .
.(II)设ξ表示一次摸奖的得分,则ξ可能的取值为0,1,2.
 ;
;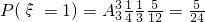 ;
;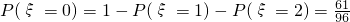 ∴一次摸奖得分ξ的分布列为
∴一次摸奖得分ξ的分布列为| ξ | 2 | 1 | 0 |
| P |  |  | 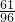 |
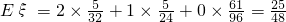 .
.分析:(I)每次有放回地抽取,取到红球的概率为
 ;取到白球的概率为
;取到白球的概率为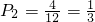 ;取到黑球的概率为
;取到黑球的概率为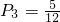 ;由此能求出一次摸奖中一等奖的概率.
;由此能求出一次摸奖中一等奖的概率.(II)设ξ表示一次摸奖的得分,则ξ可能的取值为0,1,2.
 ;
;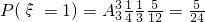 ;由此能求出一次摸奖得分ξ的分布列和期望.
;由此能求出一次摸奖得分ξ的分布列和期望.点评:本题考查n次独立重复试验恰好发生k次的概率,解题时要注意离散型随机变量ξ的分布列和期望的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目