题目内容
如图,在△ABC中,B=90°,AC=(1)异面直线AD与BC的距离;
(2)二面角A-EC-B的大小(用反三角函数表示).
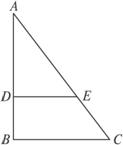
解法一:(1)在图(1)中,因![]() ,故DE∥BC.
,故DE∥BC.
又因B=90°,从而AD⊥DE.

(1)
在图(2)中,因A-DE-B是直二面角,AD⊥DE,故AD⊥底面DBCE,从而AD⊥DB.
而DB⊥BC,故DB为异面直线AD与BC的公垂线.
下求DB之长.在图(1)中,由![]() =2,得
=2,得![]() =
=![]() .
.
又已知DE=3,从而BC=![]() DE=
DE=![]() ,
,
AB=![]() =
=![]() =6.
=6.
因![]() ,故DB=2.
,故DB=2.
(2)在图(2)中,过D作DF⊥CE,交CE的延长线于F,连接AF.
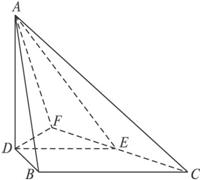
(2)
由(1)知,AD⊥底面DBCE,由三垂线定理知AF⊥FC,故∠AFD为二面角A-EC-B的平面角.
在底面DBCF中,∠DEF=∠BCE,
DB=2,EC=![]() ·
·![]() =
=![]() ,
,
因此sin∠BCE=![]() ,
,
从而在Rt△DFE中,DE=3,
DF=DEsin∠DEF=DEsin∠BCE=3·![]() =
=![]() .
.
在Rt△AFD中,AD=4,tan∠AFD=![]() =
=![]() .
.
因此所求二面角A-EC-B的大小为arctan![]() .
.
解法二:(1)同解法一.
(2)如图(3).由(1)知,以D点为坐标原点,![]() 、
、![]() 、
、![]() 的方向为x、y、z轴的正方向建立空间直角坐标系,则D(0,0,0),A(0,0,4),C(2,
的方向为x、y、z轴的正方向建立空间直角坐标系,则D(0,0,0),A(0,0,4),C(2,![]() ,0),E(0,3,0),
,0),E(0,3,0),
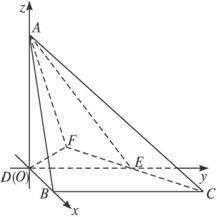
(3)
![]() =(-2,
=(-2,![]() ,0),
,0),![]() =(0,0,-4).
=(0,0,-4).
过D作DF⊥CE,交CE的延长线于F,连接AF.
设F(x0,y0,0),从而![]() =(x0,y0,0),
=(x0,y0,0),
![]() =(x0,y0-3,0).由DF⊥CE,有
=(x0,y0-3,0).由DF⊥CE,有![]() ·
·![]() =0,即2x0+
=0,即2x0+![]() y0=0.①
y0=0.①
又由![]() ∥
∥![]() ,得
,得![]() =
=![]() .②
.②
联立①②,解得x0=![]() ,y0=
,y0=![]() ,即F(
,即F(![]() ,
,![]() ,0),得
,0),得![]() =(
=(![]() ,
,![]() ,-4).
,-4).
因为![]() ·
·![]() =(
=(![]() )·(-2)+
)·(-2)+![]() ·(
·(![]() )=0,
)=0,
故AF⊥CE,又因DF⊥CE.
所以∠DFA为所求的二面角A-EC-B的平面角.
因![]() =(
=(![]() ,
,![]() ,0),有
,0),有![]() ·
·![]() =0,故AD⊥DF,△ADF为直角三角形.
=0,故AD⊥DF,△ADF为直角三角形.
|![]() |=
|=![]() =
=![]() ,|
,|![]() |=4,
|=4,
所以tan∠AFD=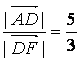 .
.
因此所求二面角A-EC-B的大小为arctan![]() .
.

 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知