题目内容
 如图,在正三棱柱中,AB=2,AA1=2由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与棱AA1的交点记为M,求:
如图,在正三棱柱中,AB=2,AA1=2由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与棱AA1的交点记为M,求:(1)该最短路线的长及
| A1M | AM |
(2)平面C1MB与平面ABC所成二面角(锐角)
分析:(1)将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点D的位置,连接DC1交AA1于M,则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线,求出DC1和
的值即可;
(2)连接DB,C1B,可证∠C1BC就是平面C1MB与平面ABC所成二面角的平面角,在三角形C1BC中求出此角.
| A1M |
| AM |
(2)连接DB,C1B,可证∠C1BC就是平面C1MB与平面ABC所成二面角的平面角,在三角形C1BC中求出此角.
解答:解:(1)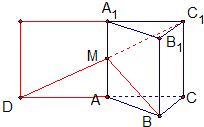 如图,将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点D的位置,连接DC1交AA1于M,
如图,将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点D的位置,连接DC1交AA1于M,
则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线,
其长为
=
=2
∵△DMA≌△C1MA1,
∴AM=A1M
故
=1
(2)连接DB,C1B,
则DB就是平面C1MB与平面ABC的交线在△DCB中,
∵∠DBC=∠CBA+∠ABD=60°+30°=90°,
∴CB⊥DB,
又C1C⊥平面CBD,
由三垂线定理得C1B⊥DB,∴∠C1BC就是平面C1MB与平面ABC所成二面角的平面角(锐角),
∵侧面C1B1BC是正方形,∴∠C1BC=45°,
故平面C1MB与平面ABC所成的二面角(锐角)为45°.
 如图,将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点D的位置,连接DC1交AA1于M,
如图,将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点D的位置,连接DC1交AA1于M,则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线,
其长为
| DC2+CC12 |
| 42+22 |
| 5 |
∵△DMA≌△C1MA1,
∴AM=A1M
故
| A1M |
| AM |
(2)连接DB,C1B,
则DB就是平面C1MB与平面ABC的交线在△DCB中,
∵∠DBC=∠CBA+∠ABD=60°+30°=90°,
∴CB⊥DB,
又C1C⊥平面CBD,
由三垂线定理得C1B⊥DB,∴∠C1BC就是平面C1MB与平面ABC所成二面角的平面角(锐角),
∵侧面C1B1BC是正方形,∴∠C1BC=45°,
故平面C1MB与平面ABC所成的二面角(锐角)为45°.
点评:本小题主要考查直线与平面的位置关系、棱柱等基本知识,考查空间想象能力、逻辑思维能力和运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

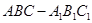 中,
中, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的动点(与端点不重合),且
上的动点(与端点不重合),且 .
.
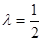 ,求证:
,求证: ;
; 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值. 中,D为棱
中,D为棱 的中点,若截面
的中点,若截面 是面积为6的直角三角形,则此三棱柱的体积为
。
是面积为6的直角三角形,则此三棱柱的体积为
。
 中,
中,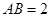 .若二面角
.若二面角 的大小为
的大小为 ,则点
,则点 到平面
到平面 的距离为
。
的距离为
。 