题目内容
(本小题满分12分)
设函数

(1)求函数 的单调区间、极值;
的单调区间、极值;
(2)若当 时,恒有
时,恒有 ,试确定
,试确定 的取值范围。
的取值范围。
(1)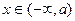 时 ,
时 , 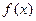 单调递减;
单调递减;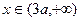
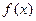 单调递减;
单调递减;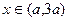
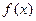 单调递
单调递 增
增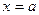 时
时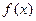 有极小值
有极小值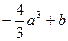 ,
,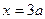 时
时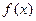 有极大值b
有极大值b
(2)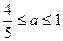
解析(1)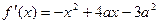 ,
,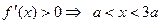
所以,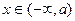 时 ,
时 , 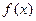 单调递减;
单调递减;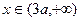
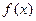 单调递减;
单调递减;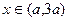
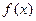 单调递
单调递 增。
增。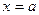 时
时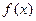 有极小值
有极小值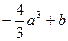 ,
,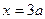 时
时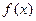 有极大值b
有极大值b
(2) 由 得:
得: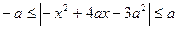
因为 所以
所以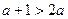 所以
所以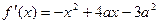 在
在 上为减函数。
上为减函数。
所以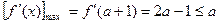 ,
,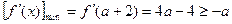
即: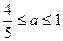

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目

 的对称轴方程;
的对称轴方程; 时,若函数
时,若函数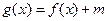 有零点,求m的范围;
有零点,求m的范围; ,
, ,求
,求 的值.
的值.  分)
分)
 是偶函数.
是偶函数. 的值,并给出函数
的值,并给出函数 的单调区间(不要求证明);
的单调区间(不要求证明); 为实常数,解关于
为实常数,解关于 的不等式:
的不等式:
 都满足不等式
都满足不等式 的所有函数
的所有函数 组成的集合记为M,例如,函数
组成的集合记为M,例如,函数 。
。 ,证明:
,证明: ;
; ,并说明理由;
,并说明理由;
 是定义域在(-1,1)上的奇函数,且
是定义域在(-1,1)上的奇函数,且 .
. 的解析式;
的解析式; .
. ;
; 时,由图象写出f(x)的最小值
时,由图象写出f(x)的最小值 是定义在
是定义在 上的增函数,对于任意的
上的增函数,对于任意的 ,都有
,都有 ,且满足
,且满足 .
. 的值;
的值;  的
的 的取值范围.
的取值范围. 是定义域为R上的奇函数。
是定义域为R上的奇函数。 的值.
的值. 上的最小值为—2,求m的值。
上的最小值为—2,求m的值。 ,当
,当 恒成立的a的最小值为k,存在n个
恒成立的a的最小值为k,存在n个 ,且
,且 ,任取n个自变量的值
,任取n个自变量的值

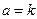 ,且存在n个自变量的值
,且存在n个自变量的值 ,使
,使 ,求证:
,求证: