题目内容
已知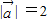 ,
, ,
,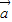 与
与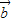 的夹角为45°,要使
的夹角为45°,要使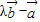 与
与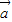 垂直,则λ= .
垂直,则λ= .
【答案】分析:由已知中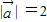 ,
,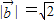 ,
,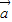 与
与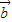 的夹角为45°,代入向量数量积公式,我们可以计算出
的夹角为45°,代入向量数量积公式,我们可以计算出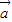 •
• 值,又由
值,又由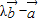 与
与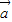 垂直,即(
垂直,即(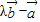 )•
)•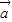 =0,我们可以构造出一个关于λ的方程,解方程即可求出满足条件的λ值.
=0,我们可以构造出一个关于λ的方程,解方程即可求出满足条件的λ值.
解答:解:∵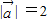 ,
,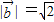 ,
,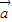 与
与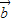 的夹角为45°,
的夹角为45°,
∴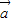 •
•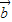 =2•
=2•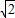 •cos45°=2
•cos45°=2
若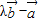 与
与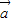 垂直,
垂直,
则(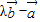 )•
)•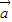 =λ(
=λ(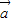 •
•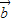 )-
)-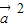 =2λ-4=0
=2λ-4=0
解得λ=2
故答案为:2
点评:本题考查的知识点是数量积判断两个平面向量的垂直关系,平面向量数量积的性质及其运算,其中根据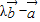 与
与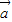 垂直,则其数量积(
垂直,则其数量积(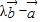 )•
)•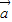 =0,构造出一个关于λ的方程,是解答本题的关键.
=0,构造出一个关于λ的方程,是解答本题的关键.
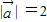 ,
,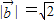 ,
,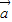 与
与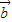 的夹角为45°,代入向量数量积公式,我们可以计算出
的夹角为45°,代入向量数量积公式,我们可以计算出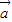 •
• 值,又由
值,又由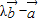 与
与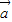 垂直,即(
垂直,即(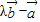 )•
)•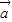 =0,我们可以构造出一个关于λ的方程,解方程即可求出满足条件的λ值.
=0,我们可以构造出一个关于λ的方程,解方程即可求出满足条件的λ值.解答:解:∵
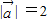 ,
,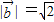 ,
,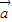 与
与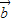 的夹角为45°,
的夹角为45°,∴
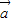 •
•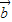 =2•
=2•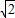 •cos45°=2
•cos45°=2若
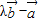 与
与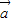 垂直,
垂直,则(
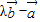 )•
)•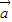 =λ(
=λ(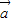 •
•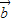 )-
)-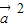 =2λ-4=0
=2λ-4=0解得λ=2
故答案为:2
点评:本题考查的知识点是数量积判断两个平面向量的垂直关系,平面向量数量积的性质及其运算,其中根据
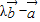 与
与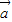 垂直,则其数量积(
垂直,则其数量积(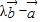 )•
)•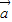 =0,构造出一个关于λ的方程,是解答本题的关键.
=0,构造出一个关于λ的方程,是解答本题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 |=|
|=|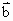 |=1,
|=1,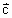 =2
=2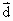 =k
=k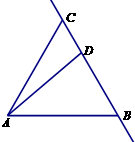 已知|
已知| |=|
|=| |=1,
|=1, ,如图,
,如图, =5
=5 =2
=2 =2
=2 ,则|
,则| |=________.
|=________.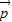 |=|
|=|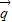 |=1,
|=1,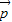 与
与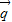 的夹角为
的夹角为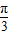 ,如图,
,如图,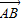 =5
=5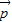 -
-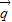 ,
,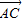 =2
=2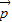 +4
+4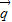 ,
,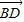 =2
=2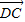 ,则|
,则|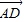 |= .
|= .