题目内容
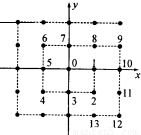 如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字0,点(1,0)处标数字1,点(1,-1)处标数字2,点(0,-1)处标数字3,点(-1,-1)处标数字4,点(-1,0)处标数字5,点(-1,1)处标数字6,点(0,1)处标数字7,…以此类推,
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字0,点(1,0)处标数字1,点(1,-1)处标数字2,点(0,-1)处标数字3,点(-1,-1)处标数字4,点(-1,0)处标数字5,点(-1,1)处标数字6,点(0,1)处标数字7,…以此类推,①标数字50的格点的坐标为 .
②记格点坐标为(m,n)的点(m、n均为正整数)处所标的数字为f(m,n),若n>m,则f(m,n)= .
【答案】分析:由图形,格点的连线呈周期性过横轴,研究每一周的格点数及每一行每一列格点数的变化,得出规律即可
解答:解:从横轴上的点开始点开始计数,从1开始计数第一周共9个格点,除了四个顶点外每一行第一列各有一个格点,外加一个延伸点
第二周从10开始计,除了四个顶点的四个格点外,每一行每一列有三个格点,外加一个延伸点共17个,
拐弯向下到达横轴前的格点补开始点的上面以补足起始点所在列的个数,
由此其规律是后一周是前一周的格点数加上8×(周数-1)
令周数为t,各周的点数和为St=9+8(t-1)=8t+1,每一行(或列)除了端点外的点数与周数的关系是b=2t-1
由于S1=9,S2=17,S3=25,S4=33,
①由于9+17+25=51,第50个格点应在第三周的倒数第二个点上,故其坐标为(4,2)
②f(1,0)=12,f(2,1)=32,f(3,2)=52,…,f(n+1,n)=(2n+1)2.∵n>m,∴n≥m-1,∴当n>m时,f(m,n)=(2n+1)2+m-n-1.
故答案为(4,2),2n+1)2+m-n-1,(n>m)
点评:本题考查归纳推理,归纳推理是由特殊到一般的推理,求解本题的关键是从特殊数据下手,找出规律,总结出所要的表达式,如本题的第二个填空.归纳在现实生活在有着十分广泛的运用,应好好把握其推理模式.
解答:解:从横轴上的点开始点开始计数,从1开始计数第一周共9个格点,除了四个顶点外每一行第一列各有一个格点,外加一个延伸点
第二周从10开始计,除了四个顶点的四个格点外,每一行每一列有三个格点,外加一个延伸点共17个,
拐弯向下到达横轴前的格点补开始点的上面以补足起始点所在列的个数,
由此其规律是后一周是前一周的格点数加上8×(周数-1)
令周数为t,各周的点数和为St=9+8(t-1)=8t+1,每一行(或列)除了端点外的点数与周数的关系是b=2t-1
由于S1=9,S2=17,S3=25,S4=33,
①由于9+17+25=51,第50个格点应在第三周的倒数第二个点上,故其坐标为(4,2)
②f(1,0)=12,f(2,1)=32,f(3,2)=52,…,f(n+1,n)=(2n+1)2.∵n>m,∴n≥m-1,∴当n>m时,f(m,n)=(2n+1)2+m-n-1.
故答案为(4,2),2n+1)2+m-n-1,(n>m)
点评:本题考查归纳推理,归纳推理是由特殊到一般的推理,求解本题的关键是从特殊数据下手,找出规律,总结出所要的表达式,如本题的第二个填空.归纳在现实生活在有着十分广泛的运用,应好好把握其推理模式.

练习册系列答案
相关题目
 (2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知
(2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知 将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知
将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知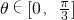 .
. 的坐标(要求将结果化简为形如(cosα,sinα)的形式);
的坐标(要求将结果化简为形如(cosα,sinα)的形式);

 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,