题目内容
(本小题满分12分)
设函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]()
(I)求![]() 的取值范围,并讨论
的取值范围,并讨论![]() 的单调性;
的单调性;
(II)证明:![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
:(Ⅰ)因为![]() ,设
,设![]() ,
,
依题意知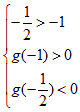 得
得![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]()
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以函数的单调递增区间为![]() 和
和![]() ,单调递减区间
,单调递减区间![]() ,
,
其中,![]() 且
且![]() .
.
(Ⅱ)证明:由(Ⅰ)知![]() ,设
,设![]() ,
,
![]()
所以![]() 在
在![]() 递减,又
递减,又![]() 在
在![]() 处连续,所以
处连续,所以![]() ,
,
即![]() .
.
解析:
:(Ⅰ)首先求出函数的导数,因为原函数有两个极值点,所以导函数有两个不同解,因为真数![]() ,所以两个根都要在定义域内,这样就转化为了一元二次方程根分布问题,求出
,所以两个根都要在定义域内,这样就转化为了一元二次方程根分布问题,求出![]() 的取值范围.
的取值范围.
利用![]() 求得函数的的单调递增区间,利用
求得函数的的单调递增区间,利用![]() 求出单间区间.一定注意单调区间在定义域内.
求出单间区间.一定注意单调区间在定义域内.
(II)因为![]() 不确定,
不确定,![]() 就不确定,它是参数
就不确定,它是参数![]() 函数,要使
函数,要使![]() 恒成立,只需
恒成立,只需![]() 的最小值大于
的最小值大于![]() 即可.把恒成立问题转化为求函数的最值来解决,求函数的最值还是用导数.
即可.把恒成立问题转化为求函数的最值来解决,求函数的最值还是用导数.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目