题目内容
一台仪器每启动一次都随机地出现一个10位的二进制数A=a1a2a3…a10,其中A的各位数字中,a1=1,ak(k=2,3,…,10)出现0的概率为| 1 |
| 3 |
| 2 |
| 3 |
分析:由题意知本题是一个独立重复试验,由a1=1知,只需考虑剩余9个位置,可分成两类:第一类,4个0连排出现在左、右两端时(左端时紧挨a1),共有4×2=8种;第二类,4个0连排左右两边都有1时,共有4×3=12种.
解答:解:∵a1=1,
∴只需考虑剩余9个位置,可分成两类:
第一类,4个0连排出现在左、右两端时(左端时紧挨a1),共有4×2=8种;
第二类,4个0连排左右两边都有1时,共有4×3=12种,
∴S=5,有且仅有4个0连排在一起的概率P=(8+12)×(
)4(
)5
∴P=
,
故答案为:
.
∴只需考虑剩余9个位置,可分成两类:
第一类,4个0连排出现在左、右两端时(左端时紧挨a1),共有4×2=8种;
第二类,4个0连排左右两边都有1时,共有4×3=12种,
∴S=5,有且仅有4个0连排在一起的概率P=(8+12)×(
| 2 |
| 3 |
| 1 |
| 3 |
∴P=
| 320 |
| 39 |
故答案为:
| 320 |
| 39 |
点评:考查学生计数原理、排列组合知识,同时还要将实际的情景进行适当的转化.注意试验是在同样条件下进行的,各次之间相互独立的一种试验.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
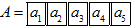 ,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为