题目内容
一台仪器每启动一次都随机地出现一个5位的二进制数A=a1a2a3a4a5,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为| 1 |
| 3 |
| 2 |
| 3 |
(1)求ξ=3的概率;
(2)求ξ的概率分布列;
(3)若启动一次出现的数字为A=10101则称这次试验成功,求5次重复试验成功的次数的期望.
分析:(1)此题需要进行转化,不能直接套公式,由a1=1,可知有一次的试验结果已经确定;当ξ=3时的概率,相当于在后面的4个数中出现2个1,计算可得答案;
(2)分析ξ的取值情况,结合变量对应的事件和独立重复试验的概率公式,做出变量对应的概率,并列出ξ值的分布列,
(3)由题意知变量符合二项分布,根据成功概率和实验的次数,用二项分布的期望公式得到结果.
(2)分析ξ的取值情况,结合变量对应的事件和独立重复试验的概率公式,做出变量对应的概率,并列出ξ值的分布列,
(3)由题意知变量符合二项分布,根据成功概率和实验的次数,用二项分布的期望公式得到结果.
解答:解:(1)由题意知数字出现的次数符合独立重复试验,
当ξ=3时的概率,相当于在后面的4个数中出现2个1,
p(ξ=3)=
(
)2•(
)2=
(2)ξ的可能取值为1,2,3,4,5,
p(ξ=1)=(
)4=
p(ξ=2)=
(
)3•(
)=
p(ξ=3)=
(
)2•(
)2=
p(ξ=4)=
(
)3•(
)=
p(ξ=5)=(
)4=
∴ξ的分布列为:
(3)启动一次出现数字为A=|0|0|的概率P=(
)2(
)2=
由题意知变量符合二项分布,
根据成功概率和实验的次数的值,
有η~B(5,
)
∴η的数学期望为Eη=
.
当ξ=3时的概率,相当于在后面的4个数中出现2个1,
p(ξ=3)=
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 24 |
| 81 |
(2)ξ的可能取值为1,2,3,4,5,
p(ξ=1)=(
| 1 |
| 3 |
| 1 |
| 81 |
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 81 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 24 |
| 81 |
| C | 3 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 32 |
| 81 |
| 2 |
| 3 |
| 16 |
| 81 |
∴ξ的分布列为:
| ξ | 1 | 2 | 3 | 4 | 5 | ||||||||||
| p |
|
|
|
|
|
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 81 |
由题意知变量符合二项分布,
根据成功概率和实验的次数的值,
有η~B(5,
| 4 |
| 81 |
∴η的数学期望为Eη=
| 20 |
| 81 |
点评:本题考查的知识点是n次独立重复试验中恰好发生k次的概率,由a1=1,将ξ=n,转化为后面的4个数中出现n-1个1是解答本题的关键.

练习册系列答案
相关题目
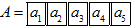 ,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为