题目内容
一台仪器每启动一次都随机地出现一个5位的二进制数A=a1a2a3a4a5,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为
,出现1的概率为
.例如:A=10001,其中a1=a5=1,a2=a3=a4=0.记ξ=a1+a2+a3+a4+a5,当启动仪器一次时
(Ⅰ)求ξ=3的概率;
(Ⅱ)求ξ的概率分布列及Eξ
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅰ)求ξ=3的概率;
(Ⅱ)求ξ的概率分布列及Eξ
分析:(Ⅰ)由题意得:P(ξ=3)=
•(
)2•(
)2,由此能求出ξ=3的概率.
(Ⅱ)由题设知,ξ的可能取值为1,2,3,4,5,分别求出P(ξ=1),P(ξ=2),P(ξ=3),P(ξ=4),P(ξ=5),由此能求出ξ的概率分布列和Eξ.
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅱ)由题设知,ξ的可能取值为1,2,3,4,5,分别求出P(ξ=1),P(ξ=2),P(ξ=3),P(ξ=4),P(ξ=5),由此能求出ξ的概率分布列和Eξ.
解答:解:(Ⅰ)由题意得:P(ξ=3)=
•(
)2•(
)2=
.
(Ⅱ)由题设知,ξ的可能取值为1,2,3,4,5,
且P(ξ=1)=
(
)4=
,
P(ξ=2)=
(
)3(
) =
,
P(ξ=3)=
(
)2(
)2=
,
P(ξ=4)=
(
) (
)3=
,
P(ξ=5)=
(
)4=
,
故ξ的概率分布列为:
∴Eξ=1×
+2×
+3×
+4×
+5×
=
.
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
(Ⅱ)由题设知,ξ的可能取值为1,2,3,4,5,
且P(ξ=1)=
| C | 0 4 |
| 1 |
| 3 |
| 1 |
| 81 |
P(ξ=2)=
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 81 |
P(ξ=3)=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 24 |
| 81 |
P(ξ=4)=
| C | 3 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 32 |
| 81 |
P(ξ=5)=
| C | 4 4 |
| 2 |
| 3 |
| 16 |
| 81 |
故ξ的概率分布列为:
| ξ | 1 | 2 | 3 | 4 | 5 | ||||||||||
P |
|
|
|
|
|
| 1 |
| 81 |
| 8 |
| 81 |
| 24 |
| 81 |
| 32 |
| 81 |
| 16 |
| 81 |
| 11 |
| 3 |
点评:本题考查离散型随机变量的概率分布列和数学期望,是中档题.解题时要认真审题,仔细解答,注意概率知识的灵活运用.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
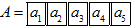 ,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数字中,a1=1,ak(k=2,3,4,5)出现0的概率为