题目内容
 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3(Ⅰ)设点O是AB的中点,证明:OC∥平面A1B1C1;
(Ⅱ)求二面角B-AC-A1的大小.
分析:(Ⅰ)作OD∥AA1交A1B1于D,连C1D,根据梯形中位线定理及平行四边形判定定理,可得四边形ODC1C是平行四边形,进而OC∥C1D,根据线面平行的判定定理,可得OC∥平面A1B1C1.
(Ⅱ)以B1为原点建立空间直角坐标系,求出平面ABC的一个法向量和平面AA1C1C的一个法向量,代入向量夹角公式,求出二面角B-AC-A1平面角的余弦值,进而可得二面角B-AC-A1的大小.
(Ⅱ)以B1为原点建立空间直角坐标系,求出平面ABC的一个法向量和平面AA1C1C的一个法向量,代入向量夹角公式,求出二面角B-AC-A1平面角的余弦值,进而可得二面角B-AC-A1的大小.
解答: 证明:(Ⅰ)作OD∥AA1交A1B1于D,连C1D
证明:(Ⅰ)作OD∥AA1交A1B1于D,连C1D
则OD∥BB1∥CC1
因为O是AB的中点,
所以OD=
(AA1+BB1)=3=CC1
则四边形ODC1C是平行四边形,
因此有OC∥C1D,C1D?平面C1B1A1
且OC?平面C1B1A1,
则OC∥平面A1B1C1…6′
(Ⅱ)如图,以B1为原点建立空间直角坐标系,
则A(0,1,4),B(0,0,2),C(1,0,3),
∴
=(0,-1,-2),
=(1,0,1),
设
=(x,y,z)是平面ABC的一个法向量,则
则
•
=0,
•
=0得:
取x=-z=1,
=(1,2,-1)
显然,
=(1,1,0)为平面AA1C1C的一个法向量
则cos?
,
>=
=
=
,
结合图形可知所求二面角为锐角
所以二面角B-AC-A1的大小是30°…12′
 证明:(Ⅰ)作OD∥AA1交A1B1于D,连C1D
证明:(Ⅰ)作OD∥AA1交A1B1于D,连C1D则OD∥BB1∥CC1
因为O是AB的中点,
所以OD=
| 1 |
| 2 |
则四边形ODC1C是平行四边形,
因此有OC∥C1D,C1D?平面C1B1A1
且OC?平面C1B1A1,
则OC∥平面A1B1C1…6′
(Ⅱ)如图,以B1为原点建立空间直角坐标系,

则A(0,1,4),B(0,0,2),C(1,0,3),
∴
| AB |
| BC |
设
| m |
则
| AB |
| m |
| BC |
| m |
|
取x=-z=1,
| m |
显然,
| n |
则cos?
| m |
| n |
| ||||
|
|
| 1+2+0 | ||||
|
| ||
| 2 |
结合图形可知所求二面角为锐角
所以二面角B-AC-A1的大小是30°…12′
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,其中(I)的关键是证得OC∥C1D,(II)的关键是构造空间坐标系,将二面角问题转化为向量夹角问题.

练习册系列答案
相关题目
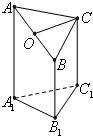 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3. 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3. 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
 ? 若存在,确定
? 若存在,确定 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.