题目内容
 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.(I)设点O是AB的中点,证明:OC∥平面A1B1C1;
(II)求此几何体的体积;
(Ⅲ)点F为AA1上一点,若BF⊥平面COB1,求AF的长.
分析:(I)借助线面平行的判定定理证明OC∥平面A1B1C1.证明OC平行于平面A1B1C1内的一条直线即可;
(II)以同样大的几何体,进行补形,可得一直三棱柱,底面为△A1B1C1,高为6,从而可求求几何体体积;
(Ⅲ)建立如图所示的空间直角坐标系,用坐标表示点与向量,利用若BF⊥平面COB1,则BF⊥B1C,即可求得结论.
(II)以同样大的几何体,进行补形,可得一直三棱柱,底面为△A1B1C1,高为6,从而可求求几何体体积;
(Ⅲ)建立如图所示的空间直角坐标系,用坐标表示点与向量,利用若BF⊥平面COB1,则BF⊥B1C,即可求得结论.
解答: (I)证明:作OD∥AA1交A1B1于D,连C1D,则OD∥BB1∥CC1.
(I)证明:作OD∥AA1交A1B1于D,连C1D,则OD∥BB1∥CC1.
∵O是AB的中点,∴OD=
=3=CC1.
∴ODC1C是平行四边形,∴OC∥C1D.
∵C1D?平面A1B1C1且OC?平面A1B1C1,
∴OC∥面A1B1C1.
(II)以同样大的几何体,进行补形,可得一直三棱柱,底面为△A1B1C1,高为6
∴所求几何体体积为V=
×
×2×2×6=6
(Ⅲ)建立如图所示的空间直角坐标系,则B1(0,0,0),B(0,0,2),C(0,2,3),
设F(2,0,m),则
=(0,2,3),
=(2,0,m-2)
若BF⊥平面COB1,则BF⊥B1C,∴m=2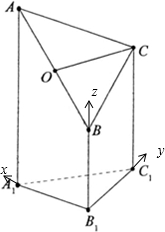
∴AF=2
 (I)证明:作OD∥AA1交A1B1于D,连C1D,则OD∥BB1∥CC1.
(I)证明:作OD∥AA1交A1B1于D,连C1D,则OD∥BB1∥CC1.∵O是AB的中点,∴OD=
| AA1+BB1 |
| 2 |
∴ODC1C是平行四边形,∴OC∥C1D.
∵C1D?平面A1B1C1且OC?平面A1B1C1,
∴OC∥面A1B1C1.
(II)以同样大的几何体,进行补形,可得一直三棱柱,底面为△A1B1C1,高为6
∴所求几何体体积为V=
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)建立如图所示的空间直角坐标系,则B1(0,0,0),B(0,0,2),C(0,2,3),
设F(2,0,m),则
| B1C |
| BF |
若BF⊥平面COB1,则BF⊥B1C,∴m=2

∴AF=2
点评:本题考查线面平行,考查几何体的条件,考查线面垂直,掌握线面平行的判定,合理补形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
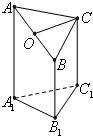 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3. 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
 ? 若存在,确定
? 若存在,确定 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.