题目内容
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中, 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.

(1)求证:EM∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面 ? 若存在,确定
? 若存在,确定
点N的位置;若不存在,请说明理由.
【答案】
(1)详见解析;(2)存在,
【解析】
试题分析:(1)要证明直线和平面平行,只需证明直线和平面内的一条直线平行即可,该题取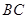 中点
中点 ,连
,连 ,先证
,先证 ,则四边形
,则四边形 是平行四边形,从而
是平行四边形,从而 ,进而证明
,进而证明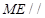 面
面 ;(2)假设
;(2)假设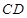 上存在满足条件的点
上存在满足条件的点 ,此时面
,此时面 内必存在垂直于
内必存在垂直于 的两条直线,容易证明
的两条直线,容易证明 面
面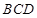 ,所以
,所以 ,又
,又 ,所以
,所以 ,接下来再能保证
,接下来再能保证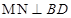 即可,此时必有
即可,此时必有 ∽
∽ ,进而根据成比例线段可求出
,进而根据成比例线段可求出 的长度,即点
的长度,即点 的位置确定.
的位置确定.
试题解析: (Ⅰ)取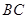 中点
中点 ,连
,连
 ,又因为
,又因为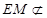 面
面 ,而
,而 面
面 ,所以
,所以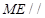 面
面 ;
;

(2)在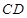 上取点
上取点 使
使 ,连接
,连接
 ,
, ,又
,又 面
面
所以 ,又因为
,又因为 ,所以
,所以 面
面 ,所以
,所以 ,又
,又 ,所以
,所以 ,故
,故 面
面 .
.
考点:1、直线和平面平行的判定;2、三角形的相似;3、线面垂直的判定和性质.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
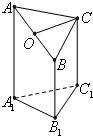 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3. 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3. 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.