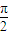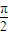题目内容
若函数f(x)=e-(x-u)2(e是自然对数的底数)的最大值是m,且f(x)是偶函数,则m+μ=分析:由f(x)是偶函数可知f(-1)=f(1),代入可求u=0,所以f(x)=e-x2,所以当x=0时函数f(x)取得最大值,从而可求.
解答:解:∵f(x)是偶函数,
∴f(-1)=f(1),
∴u=0
∴f(x)=e-x2,
∴当x=0时函数f(x)取得最大值,且最大值为1,
∴m+μ=1.
故答案为:1.
∴f(-1)=f(1),
∴u=0
∴f(x)=e-x2,
∴当x=0时函数f(x)取得最大值,且最大值为1,
∴m+μ=1.
故答案为:1.
点评:本题主要考查函数的奇偶性问题.另外涉及到指数函数的最值问题,这在考试中经常遇到.

练习册系列答案
相关题目
若函数f(x)=e-xsinx,则此函数图象在点(4,f(4))处的切线的倾斜角为( )
A、
| ||
| B、0 | ||
| C、钝角 | ||
| D、锐角 |