题目内容
(本大题16分)
设![]() 为实数,函数f(x)=x|x–a|,其中xÎR。
为实数,函数f(x)=x|x–a|,其中xÎR。
(1)分别写出当a=0.a=2.a= –2时函数f(x)的单调区间;
(2)判断函数f(x)的奇偶性,并加以证明。
(1) 当a=0时,f(x)=x|x|=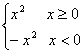 ,
,
f(x)的单调递增区间为![]() ;…2分
;…2分
当a=2时,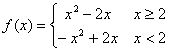
![]() 的单调递增区间为(–∞,1)和(2,+∞);…………………………………………4分
的单调递增区间为(–∞,1)和(2,+∞);…………………………………………4分
![]() 的单调递减区间为(1,2)………………………………………………………6分
的单调递减区间为(1,2)………………………………………………………6分
当a= –2时,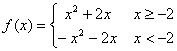
![]() 的单调递增区间为(–∞, –2)和(–1, +∞);……………………………………8分
的单调递增区间为(–∞, –2)和(–1, +∞);……………………………………8分
![]() 的单调递减区间为(–2,–1)…………………………………………………10分
的单调递减区间为(–2,–1)…………………………………………………10分
(2)当a=0时,f(x)=x|x|,所以f(x)为奇函数…………………………………11分
因为定义域为R关于原点对称,且f(–x)=–x|–x|=–f(x)
所以![]() 为奇函数。…………………………………………………………………13分
为奇函数。…………………………………………………………………13分
当a¹0时,f(x)=x|x–a|为非奇非偶函数,………………………………………14分
f(a)=0,f(–a)= –a|2a|,所以f(–a) ¹ f(a),f(–a) ¹ – f(a)
所以f(x)是非奇非偶函数。………………………………………16分

练习册系列答案
相关题目