题目内容
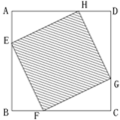 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )分析:先根据题意,证明△AEH≌△BFE,再求出小正方形的边长,进而可求其面积,进一步可求s关于x的函数图象
解答:解:因为∠AEF=∠AEH+∠FEH=∠BFE+∠B
所以∠AEH=∠BFE
因为EH=EF,∠A=∠B=90°
所以△AEH≌△BFE
所以AH=BE 设AE=x,所以AH=BE=1-x
∴s=EH2=AE2+AH2=x2+(1-x)2
∴s=2x2-2x+1
=2[x-
]2+
所以当x=
时,即E在AB的中点时,s有最小值
图象为开口向上的抛物线,顶点坐标为(
,
)
故选B.
所以∠AEH=∠BFE
因为EH=EF,∠A=∠B=90°
所以△AEH≌△BFE
所以AH=BE 设AE=x,所以AH=BE=1-x
∴s=EH2=AE2+AH2=x2+(1-x)2
∴s=2x2-2x+1
=2[x-
| 1 |
| 2 |
| 1 |
| 2 |
所以当x=
| 1 |
| 2 |
| 1 |
| 2 |
图象为开口向上的抛物线,顶点坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查的重点是函数的图象,解题的关键是确立函数的解析式,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图,已知圆O:x2+y2=1,O为坐标原点.
如图,已知圆O:x2+y2=1,O为坐标原点. 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a. 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= (2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.