题目内容
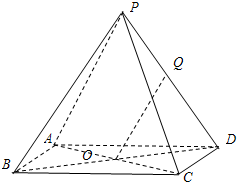 (2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.(1)求证:四棱锥P-ABCD是正四棱锥;
(2)设点Q是侧棱PD的中点,且PD的长为2a.求异面直线OQ与AB所成角的大小.(用反三角函数表示)
分析:(1)先根据PA=PC,得到PO⊥AC;同理PO⊥BD可得PO⊥平面ABCD; 再结合O是正方形ABCD的中心即可证:四棱锥P-ABCD是正四棱锥;
(2)以O为原点,正方形对角线为x,y轴,求出个对应点的坐标以及对应向量的坐标,再代入由数量积求向量夹角的计算公式即可得到结论.
(2)以O为原点,正方形对角线为x,y轴,求出个对应点的坐标以及对应向量的坐标,再代入由数量积求向量夹角的计算公式即可得到结论.
解答:解:(理)(1)连接PO,因为PA=PC,所以PO⊥AC; (2分)
同理PO⊥BD;所以PO⊥平面ABCD; (4分)
又因为O是正方形ABCD的中心,
所以四棱锥P-ABCD是正四棱锥.(6分)
(2)解:以O为原点,正方形对角线为x,y轴,A(0,-
a,0),B(
a,0,0),P(0,0,
a),
=(-
a,0,
a),
=(
a,
a,0),(10分)
设
与
的夹角为θ,则cosθ=-
.设
与
的夹角为θ,则cosθ=-
.
所以异面直线OQ与AB所成角的大小为arccos
. (14分)
同理PO⊥BD;所以PO⊥平面ABCD; (4分)
又因为O是正方形ABCD的中心,
所以四棱锥P-ABCD是正四棱锥.(6分)
(2)解:以O为原点,正方形对角线为x,y轴,A(0,-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| OQ |
| ||
| 4 |
| ||
| 4 |
| AB |
| ||
| 2 |
| ||
| 2 |
设
| OQ |
| AB |
| 1 |
| 4 |
| OQ |
| AB |
| 1 |
| 4 |
所以异面直线OQ与AB所成角的大小为arccos
| 1 |
| 4 |
点评:本题主要考查异面直线及其所成的角以及棱锥的结构特征.正四棱锥的要求是下底面为正方形,顶点在底面内的射影为下底面的中心.

练习册系列答案
相关题目