题目内容

中心在原点，焦点在x轴上的一椭圆与一双曲线有共同的焦点F1、F2，且|F1F2|=2，椭圆的长半轴与双曲线的实半轴之差为4，离心率之比为3∶7.

(1)求两曲线的方程；

(2)若P为两曲线的交点，求cos∠F1PF2.

思路分析：(1)设两曲线的方程分别为

则半焦距c=.由已知得

故所求两曲线方程分别为

(2)设∠F1PF2=θ,由余弦定理得：

｜PF1｜2+｜PF2｜2-2｜PF1｜·｜PF2｜cosθ=52　①

由椭圆定义得：｜PF1｜2+2｜PF1｜·｜PF2｜+｜PF2｜2=196　　②

由双曲线定义得：｜PF1｜2-2｜PF1｜·｜PF2｜+｜PF2｜2=36　　③

由②-①得：｜PF1｜·｜PF2｜·(1+cosθ)=72

由①-③得：｜PF1｜·｜PF2｜·(1-cosθ)=8,

∴

解得cosθ=.∴所求cos∠F1PF2=.

练习册系列答案
相关题目
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．
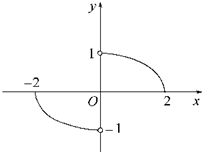精英家教网如图，函数y=f（x）的图象是中心在原点、焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{x|-
2
＜x＜0或
2
＜x≤2}
B、{x|-2≤x＜-
2
或
2
＜x≤2}
C、{x|-2≤x＜-
2
2
或
2
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}
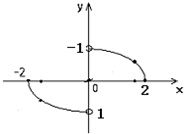精英家教网如图，函数y=f（x）的图象是中心在原点，焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{
2
2
＜x≤2或
2
2
＜x≤2}
B、{x|-2≤x＜
2
或
2
＜x≤2}
C、{x|-
2
＜x＜0或
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}

（12分）

    已知椭圆中心在原点，焦点在x轴上，长轴长等于12，离心率为.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过椭圆左顶点作直线l垂直于x轴，若动点M到椭圆右焦点的距离比它到直线l的距离小4，求点M的轨迹方程.

 
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网