题目内容
在钝角△ABC中,若B=30°,AB=2
,AC=2,则△ABC的面积是
.
| 3 |
| 3 |
| 3 |
分析:在钝角△ABC中,由余弦定理可得BC=2,再根据△ABC的面积是
AB•BC•sinB,运算求得结果.
| 1 |
| 2 |
解答:解:在钝角△ABC中,由余弦定理可得 AC2=AB2+BC2-2AB•BC•cosB,即 4=12+BC2-4
•BC•cos30°,
解得 BC=2,BC=4 (舍去,因为BC=4时,为直角三角形).
故△ABC的面积是
AB•BC•sinB=
•2
•2•sin30°=
,
故答案为
.
| 3 |
解得 BC=2,BC=4 (舍去,因为BC=4时,为直角三角形).
故△ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为
| 3 |
点评:本题主要考查余弦定理的应用,求得BC=2,是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
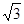 ,AC=2,则△ABC的面积是______;
,AC=2,则△ABC的面积是______; ,AC=2,则△ABC的面积是 .
,AC=2,则△ABC的面积是 .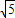 ,3)
,3)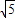 ,4)
,4)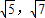 )
)