题目内容
在钝角△ABC中，若B＝30°，AB＝2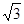
，AC＝2，则△ABC的面积是______；
【答案】
【解析】解：
解：在△ABC中，设BC=x，由余弦定理可得4=12+x2-4xcos30°，
x2-6x+8=0，∴x=2，或 x=4．(舍)
当x=2 时，△ABC的面积为
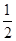AB•BC•sinB=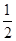×2×2×=，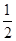
故答案为
练习册系列答案
相关题目
，AC=2，则△ABC的面积是 ．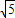
，3）
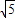，4）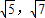
）