题目内容
已知命题 :方程
:方程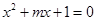 有两个不相等的负实根,命题
有两个不相等的负实根,命题 :
: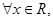
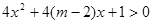 恒成立;若
恒成立;若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数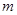 的取值范围.
的取值范围.
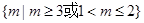 .
.
解析试题分析:先分别确定 真、
真、 真时
真时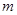 的取值范围:当
的取值范围:当 真时,只须求解不等式组
真时,只须求解不等式组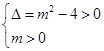 即可;当
即可;当 真时,只须求解不等式
真时,只须求解不等式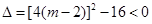 即可;然后由
即可;然后由 或
或 为真,
为真, 且
且 为假得到
为假得到 真
真 假或
假或 假
假 真,进而列出不等式组即可求出满足要求的
真,进而列出不等式组即可求出满足要求的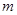 的取值范围.
的取值范围.
试题解析:当 真时,可得
真时,可得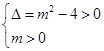 ,解之得
,解之得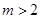
当 真时,得到:
真时,得到: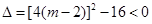 ,解之得
,解之得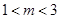
∵ 或
或 为真,
为真, 且
且 为假
为假
∴ 真
真 假或
假或 假
假 真
真
若 真
真 假时,由
假时,由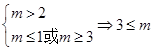
若 假
假 真时,由
真时,由
所以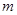 的取值范围为
的取值范围为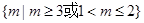 .
.
考点:1.逻辑联结词;2.二次方程根的分布问题;3.二次函数的图像与性质.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
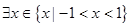 ,使等式
,使等式 成立”是真命题.
成立”是真命题. 的取值集合
的取值集合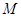 ;
; 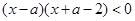 的解集为
的解集为 ,若
,若 是
是 的必要条件,求
的必要条件,求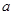 的取值范围.
的取值范围.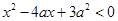 ,其中
,其中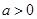 ,命题
,命题 实数
实数 满足
满足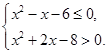 .
. 且
且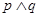 为真,求实数
为真,求实数 是
是
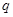 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. : 关于
: 关于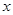 的不等式
的不等式 ,对一切
,对一切 恒成立; 命题
恒成立; 命题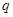 : 函数
: 函数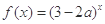 在
在 上是增函数.若
上是增函数.若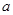 的取值范围.
的取值范围.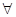 x∈[1,2],x2-a≥0,命题q:
x∈[1,2],x2-a≥0,命题q: x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.
x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.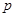 :实数
:实数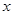 满足
满足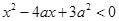 ,其中
,其中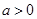 ;命题
;命题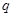 :实数
:实数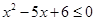 .
.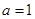 ,且
,且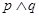 为真,求实数
为真,求实数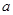 的取值范围.
的取值范围.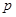 :方程
:方程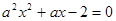 在[-1,1]上有解;命题
在[-1,1]上有解;命题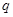 :只有一个实数
:只有一个实数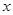 满足不等式
满足不等式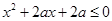 ,若命题“p或q”是假命题,求实数a的取值范围
,若命题“p或q”是假命题,求实数a的取值范围 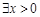 ,
,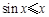 ”的否定是
”的否定是