题目内容
集合A=(―∞,―2]∪[3,+∞),关于x的不等式(x-2a)·(x+a)>0的解集为B(其中a<0).
(1)求集合B;
(2)设p:x∈A,q:x∈B,且Øp是Øq的充分不必要条件,求a的取值范围。
(1)(-∞,2a)∪(-a,+∞);(2)(―∞,-3].
解析试题分析:(1)解一元二次不等式(x-2a)·(x+a)>0,可求出B=(-∞,2a)∪(-a,+∞);
(2)依据题意有 p:x=∈(-2,3),
p:x=∈(-2,3), q∈[2a,―a],可知(-2,3)
q∈[2a,―a],可知(-2,3) [2a,―a]即
[2a,―a]即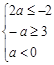 ,解得a≤-3
,解得a≤-3
试题解析:解:(1)∵a<0,2a<-a,∴B={x|x<2a或x>-a}=(-∞,2a)∪(-a,+∞)…5分
(2)∵ p:CRA=(-2,3),
p:CRA=(-2,3), q:CRB=[2a,―a]
q:CRB=[2a,―a]
由 p是
p是 q的充分不必要条件知 CRA
q的充分不必要条件知 CRA CRB 8分
CRB 8分
∴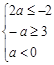
 a≤-3, 所以a的取值范围为(―∞,-3] 12分
a≤-3, 所以a的取值范围为(―∞,-3] 12分
考点:1.一元二次不等式的解法;2.必要条件、充分条件与充要条件的判断;

练习册系列答案
相关题目
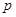 :实数
:实数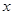 满足
满足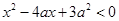 ,其中
,其中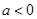 ,命题
,命题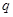 :实数
:实数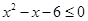 或
或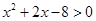 ,且
,且 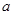 的取值范围.
的取值范围. ,命题
,命题 。
。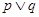 ”为真命题,“
”为真命题,“ ”为假命题,求实数x的取值范围。
”为假命题,求实数x的取值范围。 :方程
:方程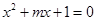 有两个不相等的负实根,命题
有两个不相等的负实根,命题 :
: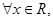
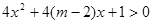 恒成立;若
恒成立;若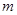 的取值范围.
的取值范围. 是
是 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.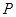 :复数
:复数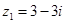 ,复数
,复数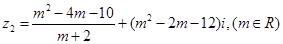 ,
, 是虚数;命题
是虚数;命题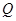 :关于
:关于 的方程
的方程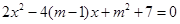 的两根之差的绝对值小于
的两根之差的绝对值小于 ;若
;若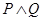 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围. 方程
方程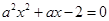 在
在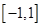 上有解,命题
上有解,命题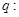 函数
函数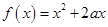
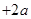 的值域为
的值域为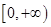 ,若命题“
,若命题“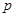 或
或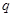 ”是假命题,求实数
”是假命题,求实数 的取值范围.
的取值范围. B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
B”; w ②“若x2+y2=0,则x,y全为0”的否命题;