题目内容
已知向量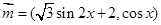 ,
,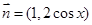 设函数
设函数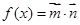 .
.
 求
求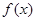 的最小正周期与单调递增区间;
的最小正周期与单调递增区间;
 在
在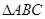 中,
中,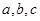 分别是角
分别是角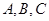 的对边,若
的对边,若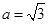 ,
,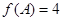 ,求
,求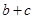 的最大值.
的最大值.
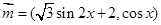 ,
,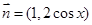 设函数
设函数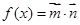 .
. 求
求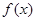 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在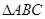 中,
中,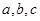 分别是角
分别是角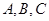 的对边,若
的对边,若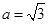 ,
,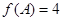 ,求
,求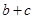 的最大值.
的最大值.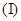
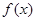 的最小正周期
的最小正周期 ,单调递增区间为
,单调递增区间为 ;
;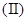
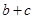 最大为
最大为 .
.试题分析:
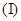 利用向量数量积的坐标运算及三角恒等变换得到
利用向量数量积的坐标运算及三角恒等变换得到 ,可得最小正周期为
,可得最小正周期为 .利用复合函数的单调性得单调递增区间
.利用复合函数的单调性得单调递增区间
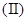 先由
先由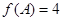 计算出
计算出 ,所以
,所以 .又
.又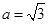 ,由正弦定理推出
,由正弦定理推出

 .或者由余弦定理得
.或者由余弦定理得 ,再由基本不等式得
,再由基本不等式得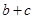 的最大值为
的最大值为 .
.试题解析:(Ⅰ)

 3分
3分∴
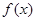 的最小正周期
的最小正周期 4分
4分由
 得
得
∴
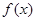 的单调递增区间为
的单调递增区间为 6分
6分(Ⅱ)由
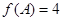 得
得 ,
,
∵
 ∴
∴ ∴
∴ ,
, 8分
8分
法一:又
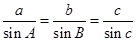 ,
,

∴当
 时,
时,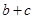 最大为
最大为 12分
12分法二:
 即
即
 ;当且仅当
;当且仅当 时等号成立. 12分
时等号成立. 12分
练习册系列答案
相关题目
 中,
中, ,
, ,
, ,
, 。
。
 表示
表示 ;
; ,
, ,
, ,分别求
,分别求 和
和 的值。
的值。 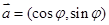 ,
,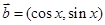 ,
,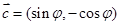 ,其中
,其中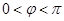 ,且函数
,且函数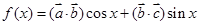 的图象过点
的图象过点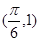 .
.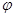 的值;
的值;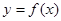 图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数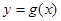 的图象,求函数
的图象,求函数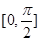 上的最大值和最小值.
上的最大值和最小值.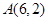 ,
,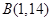 ,则与
,则与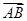 同向的单位向量为( )
同向的单位向量为( ) 或
或
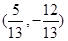
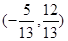 或
或 中,
中,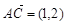 ,
,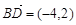 ,则该四边形的面积为( )
,则该四边形的面积为( )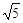
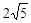
 为抛物线
为抛物线 的焦点,
的焦点, 、
、 、
、 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则 ( )
( ) 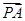 、
、 满足
满足 ,
, ,设向量
,设向量 ,则
,则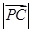 的最小值是 。
的最小值是 。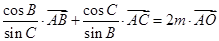 ,则m的值为( )
,则m的值为( )


 ,
, ,且
,且 ,则锐角
,则锐角 为________.
为________.