Question

已知函数f（x）的导函数如图所示，若△ABC为锐角三角形，则下列不等式一定成立的是（　　）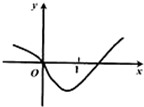

• A、f（sinA）＞f（cosA）
• B、f（sinA）＞f（cosB）
• C、f（cosA）＜f（cosB）
• D、f（sinA）＜f（cosB）

Answer 1

分析：根据函数单调性和导数之间的关系，结合三角函数值的取值范围即可得到结论．

解答：解：若△ABC为锐角三角形，则0＜A＜

π

2

，0＜B＜

π

2

，0＜C＜

π

2

，即0＜π-A-B＜

π

2

，
∴0＜

π

2

-A＜B＜

π

2

，即cos（

π

2

-A）＞cosB，
∴0＜cosB＜sinA＜1，
由导函数图象可知f（x）在（0，1）上单调递减，
∴f（sinA）＜f（cosB），
故选：D．

点评：本题主要考查函数值的大小比较，根据函数的单调性以及三角函数值的大小关系是解决本题的关键．