题目内容
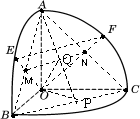
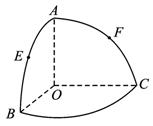
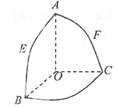
如图,O是半径为1的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,
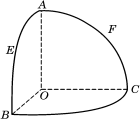
⑴求点E、F在该球面上的球面距离;
⑵求平面OEF与平面OBC所成的锐二面角.(用反三角函数表示)
答案:
解析:
解析:
|
解:⑴解法一:如图,证明0M=0N=MN= ∴点E、F在该球面上的球面距离为
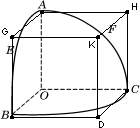
解法二:如图,补形易证:∠EOF=∠GOH=
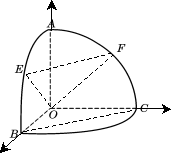
解法三:其实 解法四:如图,建立空间直角坐标系,易知E( ∴
⑵解法一:如图,取BC中点P,连接AP交MN与Q,则易证,∠POQ就是所求二面角的平面角. 在三角形OPQ中,OP= ∴∠POQ=arcos
解法二:如图,补形成正方体去解决.
解法三:如图,建立空间直角坐标系去求解.
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目