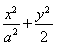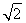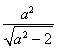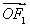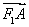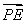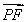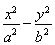Question

已知中心在坐标原点O的椭圆C经过点A(2,3)，且点F(2,0)为其右焦点．

(1)求椭圆C的方程；

(2)是否存在平行于OA的直线l，使得直线l与椭圆C有公共点，且直线OA与l的距离等于4？若存在，求出直线l的方程；若不存在，请说明理由．

 

Answer 1

（1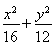）＝1（2）直线l不存在

【解析】(1)依题意，可设椭圆C的方程为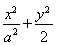＝1(a>b>0)，且可知左焦点为F′(－2,0)．

从而有解得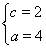

又a2＝b2＋c2，所以b2＝12，故椭圆C的方程为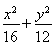＝1.

(2)假设存在符合题意的直线l，由题知直线l的斜率与直线OA的斜率相等，故可设直线l的方程为y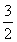＝x＋t.由得3x2＋3tx＋t2－12＝0.

因为直线l与椭圆C有公共点，所以Δ＝(3t)2－4×3(t2－12)≥0，解得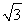－4≤t≤4.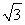

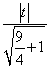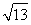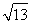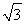另一方面，由直线OA与l的距离d＝4，可得＝4，从而t＝±2.由于±2∉[－4，4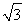]，所以符合题意的直线l不存在