题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,满足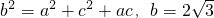 .
.
(1)求角B的大小.
(2)设角A的大小为x,△ABC的周长为y,求y=f(x)的最大值.
解:(1)∵b2=a2+c2+ac
∴cosB= =-
=-
∴B=120°
(2)由正弦定理可知 =
= =
=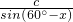 ,
,
a= •sinA=4sinx,c=
•sinA=4sinx,c= •sin(60°-x)=
•sin(60°-x)=
∴y=4sinx+4sin(60°-x)+2 =4cos(
=4cos( -30°)+2
-30°)+2 ≤4+2
≤4+2
故y的最大值为:4+2
分析:(1)把b2=a2+c2+ac代入余弦定理求得cosB的值,进而求得B.
(2)利用正弦定理分别求得a和c,进而求得三角形周长的表达式,利用和差化积公式化简整理后,利用余弦函数的性质求得最大值.
点评:本题主要考查了正弦定理和余弦定理的应用.解题的过程是通过余弦定理和正弦定理完成了边角问题的互化,达到解决问题的目的.
∴cosB=
 =-
=-
∴B=120°
(2)由正弦定理可知
 =
= =
=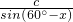 ,
,a=
 •sinA=4sinx,c=
•sinA=4sinx,c= •sin(60°-x)=
•sin(60°-x)=∴y=4sinx+4sin(60°-x)+2
 =4cos(
=4cos( -30°)+2
-30°)+2 ≤4+2
≤4+2
故y的最大值为:4+2

分析:(1)把b2=a2+c2+ac代入余弦定理求得cosB的值,进而求得B.
(2)利用正弦定理分别求得a和c,进而求得三角形周长的表达式,利用和差化积公式化简整理后,利用余弦函数的性质求得最大值.
点评:本题主要考查了正弦定理和余弦定理的应用.解题的过程是通过余弦定理和正弦定理完成了边角问题的互化,达到解决问题的目的.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |