题目内容
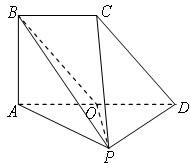 16、如图,平面ABCD⊥平面PAD,△APD是直角三角形,∠APD=90°,四边形ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=2BC,O是AD的中点
16、如图,平面ABCD⊥平面PAD,△APD是直角三角形,∠APD=90°,四边形ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=2BC,O是AD的中点(1)求证:CD∥平面PBO;
(2)求证:平面PAB⊥平面PCD.
分析:(1)因为AD=2BC,且O是AD中点,可以证四边形BCDO为平行四边形,然后根据直线与平面的判断定理进行证明;
(2)因为∠BAD=90°,所以BA⊥AD,又平面PAD⊥平面ABCD,先证明PD⊥平面PAB,再由PD?平面PCD,利用平面与平面垂直的判断定理,进行求证.
(2)因为∠BAD=90°,所以BA⊥AD,又平面PAD⊥平面ABCD,先证明PD⊥平面PAB,再由PD?平面PCD,利用平面与平面垂直的判断定理,进行求证.
解答: 证明:(1)因为AD=2BC,且O是AD中点,
证明:(1)因为AD=2BC,且O是AD中点,
所以OD=BC,又AD∥BC,所以OD∥BC,
所以四边形BCDO为平行四边形,(2分)
所以CD∥BO,CD?平面PBO,
且BO?平面PBO,故CD∥平面PBO;(6分)
(2)因为∠BAD=90°,所以BA⊥AD,
又平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,AB?平面ABCD,
∴AB⊥平面PAD,(8分)PD?平面PAD,
∴AB⊥PD,AP⊥PD,AB∩AP=A,
∴PD⊥平面PAB,(12分)∵PD?平面PCD,
故平面PAB⊥平面PCD. (14分)
 证明:(1)因为AD=2BC,且O是AD中点,
证明:(1)因为AD=2BC,且O是AD中点,所以OD=BC,又AD∥BC,所以OD∥BC,
所以四边形BCDO为平行四边形,(2分)
所以CD∥BO,CD?平面PBO,
且BO?平面PBO,故CD∥平面PBO;(6分)
(2)因为∠BAD=90°,所以BA⊥AD,
又平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,AB?平面ABCD,
∴AB⊥平面PAD,(8分)PD?平面PAD,
∴AB⊥PD,AP⊥PD,AB∩AP=A,
∴PD⊥平面PAB,(12分)∵PD?平面PCD,
故平面PAB⊥平面PCD. (14分)
点评:此题考查直线与平面平行的判断及平面与平面垂直的判断,此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
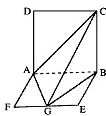 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.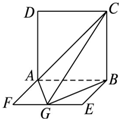 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=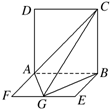 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=