题目内容
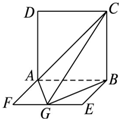 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=| 1 |
| 2 |
分析:由面面垂直的性质证明CB⊥AG,用勾股定理证明AG⊥BG,得到AG⊥平面CBG,从而面AGC⊥面BGC,在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,故∠BGH是GB与平面AGC所成的角,解Rt△CBG,可得GB与平面AGC所成角的正弦值.
解答: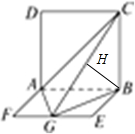 解:∵ABCD是正方形,∴CB⊥AB,
解:∵ABCD是正方形,∴CB⊥AB,
∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF.
∵AG,GB?面ABEF,∴CB⊥AG,CB⊥BG,
又AD=2a,AF=a,ABEF是矩形,G是EF的中点,
∴AG=BG=
a,AB=2a,∴AB2=AG2+BG2,∴AG⊥BG,
∵BG∩BC=B,∴AG⊥平面CBG,而AG?面AGC,故平面AGC⊥平面BGC.
在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,∴∠BGH是GB与平面AGC所成的角.
在Rt△CBG中,BH=
=
,
∵BG=
a,∴sin∠BGH=
=
.
故选C.
 解:∵ABCD是正方形,∴CB⊥AB,
解:∵ABCD是正方形,∴CB⊥AB,∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF.
∵AG,GB?面ABEF,∴CB⊥AG,CB⊥BG,
又AD=2a,AF=a,ABEF是矩形,G是EF的中点,
∴AG=BG=
| 2 |
∵BG∩BC=B,∴AG⊥平面CBG,而AG?面AGC,故平面AGC⊥平面BGC.
在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,∴∠BGH是GB与平面AGC所成的角.
在Rt△CBG中,BH=
| BC•BG |
| CG |
2
| ||
| 3 |
∵BG=
| 2 |
| BH |
| BG |
| ||
| 3 |
故选C.
点评:本题考查面面垂直的判定方法,以及线面成的角的求法,考查学生的计算能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
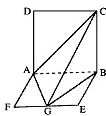 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.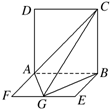 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=