题目内容
已知椭圆E的焦点在x轴上,长轴长为4,离心率为
.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)已知点A(0,1)和直线l:y=x+m,线段AB是椭圆E的一条弦且直线l垂直平分弦AB,求实数m的值.
| ||
| 2 |
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)已知点A(0,1)和直线l:y=x+m,线段AB是椭圆E的一条弦且直线l垂直平分弦AB,求实数m的值.
(Ⅰ)∵椭圆E的长轴长为4,∴a=2,离心率为
.
∴
=
,c=
,∴b=1
∵椭圆E的焦点在x轴上,
∴椭圆E的标准方程为
+y2=1;
(Ⅱ)由条件可得直线AB的方程为y=-x+1.于是,有
?5x2-8x=0?xB=
,yB=-xB+1=-
.
设弦AB的中点为M,则由中点坐标公式得xM=
,yM=
,由此及点M在直线l得
=
+m?m=-
.
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
| 3 |
∵椭圆E的焦点在x轴上,
∴椭圆E的标准方程为
| x2 |
| 4 |
(Ⅱ)由条件可得直线AB的方程为y=-x+1.于是,有
|
| 8 |
| 5 |
| 3 |
| 5 |
设弦AB的中点为M,则由中点坐标公式得xM=
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
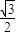 .
.