题目内容
已知点P(0,一2),椭圆c:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(1)求椭圆的方程;
(2)若椭圆上有A、B两点,使△PAB的重心为F1,求直线AB的方程;
(3)在(2)的条件下,设M为椭圆上一动点,求△MAB的面积的最大值及此时点M的坐标.
分析:(1)由三角形PF1F2的面积为2,及点P(0,一2)可得a,b的关系式,再利用a2,b2的等比中项为6
,故可求a,b;
(2)充分利用条件椭圆上有A、B两点,使△PAB的重心为F1可求;
(3)由于AB线段的长度为定值,所以要使△MAB的面积的最大值,只需点线距离最大即可.
| 2 |
(2)充分利用条件椭圆上有A、B两点,使△PAB的重心为F1可求;
(3)由于AB线段的长度为定值,所以要使△MAB的面积的最大值,只需点线距离最大即可.
解答:解:(1)由三角形PF1F2的面积为2,及点P(0,一2),可得a2-b2=1(a>b>0),
∵a2,b2的等比中项为6
,
∴a2b2=72,∴a2=9,b2=8,∴
+
=1;
(2)A(x1,y1),B(x2,y2),由椭圆上有A、B两点,使△PAB的重心为F1,可得
,
又
+
=1,
+
=1,两式相减得
=-
=
,
AB的中点为(-
,1),所以AB的方程为4x-3y+9=0.
(3)由(2)知,S△MAB=
AB×d的最大值为
+3
,此时点M的坐标为(
,-
).
∵a2,b2的等比中项为6
| 2 |
∴a2b2=72,∴a2=9,b2=8,∴
| x2 |
| 9 |
| y2 |
| 8 |
(2)A(x1,y1),B(x2,y2),由椭圆上有A、B两点,使△PAB的重心为F1,可得
|
又
| x12 |
| 9 |
| y12 |
| 8 |
| x22 |
| 9 |
| y22 |
| 8 |
| y1-y2 |
| x1-x2 |
| 8(x1+x2) |
| 9(y1+y2) |
| 4 |
| 3 |
AB的中点为(-
| 3 |
| 2 |
(3)由(2)知,S△MAB=
| 1 |
| 2 |
| 3 |
| 4 |
| 30 |
| 5 |
| 6 |
| 2 |
| 3 |
| 6 |
点评:本题考查了椭圆标准方程的求解,利用了待定系数法,求解直线方程则利用了设而不求法,要注意细细体会.

练习册系列答案
相关题目
 (a>b>0),椭圆的左右焦点分别为F1、F2,若三角形PF1F2的面积为2,且a2,b2的等比中项为6
(a>b>0),椭圆的左右焦点分别为F1、F2,若三角形PF1F2的面积为2,且a2,b2的等比中项为6 .
.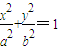 (a>b>0),椭圆的左右焦点分别为F1、F2,若三角形PF1F2的面积为2,且a2,b2的等比中项为6
(a>b>0),椭圆的左右焦点分别为F1、F2,若三角形PF1F2的面积为2,且a2,b2的等比中项为6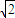 .
.