题目内容
在数1和100之间插入n个实数,使得这n+2个数构成递增的等比数列,将这n+2个数的乘积记作Tn,再令an=lgTn,n≥1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证: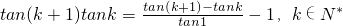 .
.
(Ⅲ)设bn=tanan•tanan+1,求数列{bn}的前n项和Sn.
(Ⅰ)解:由题意,数1和100之间插入n个实数,使得这n+2个数构成递增的等比数列,将这n+2个数的乘积记作Tn,
由等比数列的性质,序号的和相等,则项的乘积也相等知Tn= ,
,
又an=lgTn,(n≥1),
∴an=lgTn=lg =lg10n+2=n+2;
=lg10n+2=n+2;
(Ⅱ)证明:tan1=tan[(k+1)-k]=
∴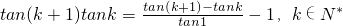
(Ⅲ)解:bn=tanan•tanan+1=tan(n+2)tan(n+3)=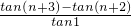 -1
-1
∴数列{bn}的前n项和Sn=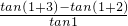 +
+ +…+
+…+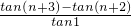 -n
-n
=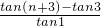 -n
-n
分析:(Ⅰ)由等比数列的性质,序号的和相等,则项的乘积也相等知Tn= ,结合an=lgTn,(n≥1),即可求数列{an}的通项公式;
,结合an=lgTn,(n≥1),即可求数列{an}的通项公式;
(Ⅱ)利用差角的正切公式,即可证得结论;
(Ⅲ)利用(Ⅱ)的结论,累加,即可求数列{bn}的前n项和Sn.
点评:本题考查等差数列与等比数列的综合,解题的关键是熟练掌握等差数列与等比数列的性质,再结合对数的运用性质得出求出数列{an}的通项公式,本题考查了综合利用知识转化变形的能力
由等比数列的性质,序号的和相等,则项的乘积也相等知Tn=
 ,
,又an=lgTn,(n≥1),
∴an=lgTn=lg
 =lg10n+2=n+2;
=lg10n+2=n+2;(Ⅱ)证明:tan1=tan[(k+1)-k]=

∴
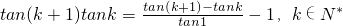
(Ⅲ)解:bn=tanan•tanan+1=tan(n+2)tan(n+3)=
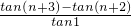 -1
-1∴数列{bn}的前n项和Sn=
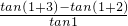 +
+ +…+
+…+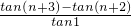 -n
-n=
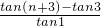 -n
-n分析:(Ⅰ)由等比数列的性质,序号的和相等,则项的乘积也相等知Tn=
 ,结合an=lgTn,(n≥1),即可求数列{an}的通项公式;
,结合an=lgTn,(n≥1),即可求数列{an}的通项公式;(Ⅱ)利用差角的正切公式,即可证得结论;
(Ⅲ)利用(Ⅱ)的结论,累加,即可求数列{bn}的前n项和Sn.
点评:本题考查等差数列与等比数列的综合,解题的关键是熟练掌握等差数列与等比数列的性质,再结合对数的运用性质得出求出数列{an}的通项公式,本题考查了综合利用知识转化变形的能力

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目