题目内容
在数1 和100之间插入n个实数,使得这n+2个数构成递增的等比数列,将这n+2个数的乘积计作Tn,再令an=lgTn,n≥1.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=tanan•tanan+1,求数列{bn}的前n项和Sn.
分析:(I)根据在数1 和100之间插入n个实数,使得这n+2个数构成递增的等比数列,我们易得这n+2项的几何平均数为10,故Tn=10n+2,进而根据对数的运算性质我们易计算出数列{an}的通项公式;
(II)根据(I)的结论,利用两角差的正切公式,我们易将数列{bn}的每一项拆成
-1的形式,进而得到结论.
(II)根据(I)的结论,利用两角差的正切公式,我们易将数列{bn}的每一项拆成
| tan(n+3)-tan(n+2) |
| tan1 |
解答:解:(I)∵在数1 和100之间插入n个实数,使得这n+2个数构成递增的等比数列,
又∵这n+2个数的乘积计作Tn,
∴Tn=10n+2
又∵an=lgTn,
∴an=lg10n+2=n+2,n≥1.
(II)∵bn=tanan•tanan+1=tan(n+2)•tan(n+3)=
-1,
∴Sn=b1+b2+…+bn=[
-1]+[
-1]+…+[
-1]
=
-n
又∵这n+2个数的乘积计作Tn,
∴Tn=10n+2
又∵an=lgTn,
∴an=lg10n+2=n+2,n≥1.
(II)∵bn=tanan•tanan+1=tan(n+2)•tan(n+3)=
| tan(n+3)-tan(n+2) |
| tan1 |
∴Sn=b1+b2+…+bn=[
| tan(4)-tan(3) |
| tan1 |
| tan(5)-tan(4) |
| tan1 |
| tan(n+3)-tan(n+2) |
| tan1 |
=
| tan(n+3)-tan(3) |
| tan1 |
点评:本题考查的知识点是等比数列的通项公式及数列与三角函数的综合,其中根据已知求出这n+2项的几何平均数为10,是解答本题的关键.

练习册系列答案
相关题目
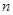 个实数,使得这
个实数,使得这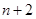 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这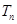 ,再令
,再令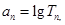
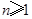 .
.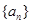 的通项公式;
的通项公式;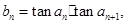 求数列
求数列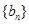 的前
的前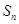 .
.