题目内容
已知椭圆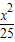
+
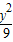=1与双曲线
-
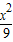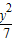=1在第一象限内的交点为P，则点P到椭圆右焦点的距离等于 ．
【答案】分析：先由椭圆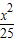
+
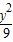=1与双曲线
-
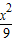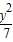=1的方程得出它们有共同的焦点F1、F2，再根据点P为椭圆和双曲线的一个交点结合定义求出|PF1|与|PF2|的表达式，代入即可求出|PF2|的值．
解答：解：因为椭圆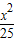
+
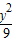=1的焦点（±4，0），与双曲线
-
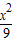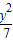=1的焦点（±4，0），
∴椭圆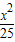
+
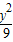=1与双曲线
-
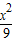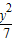=1有共同的焦点F1、F2，
设左右焦点F1、F2：
利用椭圆以及双曲线的定义可得：|PF1|+|PF2|=2×5 ①
|PF1|-|PF2|=2×3 ②
由①②得：|PF1|=8，|PF2|=2．
则点P到椭圆右焦点的距离等于 2．
故答案为：2．
点评：本题主要考查圆锥曲线的综合问题．解决本题的关键在于根据椭圆
+
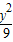=1与双曲线
-
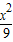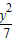=1的方程得出它们有共同的焦点F1、F2，属中档题．
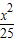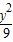+=1与双曲线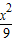-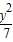=1的方程得出它们有共同的焦点F1、F2，再根据点P为椭圆和双曲线的一个交点结合定义求出|PF1|与|PF2|的表达式，代入即可求出|PF2|的值．解答：解：因为椭圆
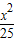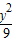+=1的焦点（±4，0），与双曲线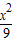-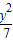=1的焦点（±4，0），∴椭圆
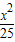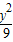+=1与双曲线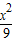-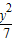=1有共同的焦点F1、F2，设左右焦点F1、F2：
利用椭圆以及双曲线的定义可得：|PF1|+|PF2|=2×5 ①
|PF1|-|PF2|=2×3 ②
由①②得：|PF1|=8，|PF2|=2．
则点P到椭圆右焦点的距离等于 2．
故答案为：2．
点评：本题主要考查圆锥曲线的综合问题．解决本题的关键在于根据椭圆
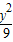+=1与双曲线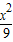-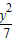=1的方程得出它们有共同的焦点F1、F2，属中档题． 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．