题目内容
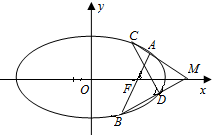 已知椭圆G:
已知椭圆G:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆G的方程;
(Ⅱ)在直线l的斜率k变化的过程中,是否存在一个常数λ,使得k1=λk恒成立?若存在,求出这个常数λ;若不存在,请说明理由.
分析:(I)由c2=a2-b2,及已知中c=1,
=
.求出a,b的值,可得椭圆G的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).联立方程后,使用韦达定理,分别求出x3,y3,x4,y4.代入斜率公式,可得k1=-k.
| c |
| a |
| ||
| 2 |
(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).联立方程后,使用韦达定理,分别求出x3,y3,x4,y4.代入斜率公式,可得k1=-k.
解答:解:(Ⅰ)设c2=a2-b2,由题意c=1,
=
.解得a=
,b=1.
∴椭圆G的方程为
+y2=1. …(5分)
(Ⅱ)存在常数λ=-1.
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).
联立
,可得(1+2k2)x2-4k2x+2(k2-1)=0
于是x1+x2=
,x1•x2=
.
直线AM的斜率t1=
,联立
,可得
(1+2t12)x2-8t12x+2(4t12-1)=0
则x1•x3=
,进一步可得x3=
.
将t1=
代入,则x3=
同理可得x4=
.
则y3=
,y4=
由
+y32=1,
+y42=1两式相减可得,
k1=-k综上可知,存在常数λ=-1. …(15分)
| c |
| a |
| ||
| 2 |
| 2 |
∴椭圆G的方程为
| x2 |
| 2 |
(Ⅱ)存在常数λ=-1.
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).
联立
|
于是x1+x2=
| 4k2 |
| 1+2k2 |
| 2(k2-1) |
| 1+2k2 |
直线AM的斜率t1=
| y1 |
| x1-2 |
|
(1+2t12)x2-8t12x+2(4t12-1)=0
则x1•x3=
| 2(4t12-1) |
| 1+2t12 |
| 2(4t12-1) |
| (1+2t12)x1 |
将t1=
| y1 |
| x1-2 |
| 3x1-4 |
| 2x1-3 |
同理可得x4=
| 3x2-4 |
| 2x2-3 |
则y3=
| -k(x1-1) |
| 2x1-3 |
| -k(x2-1) |
| 2x2-3 |
由
| x32 |
| 2 |
| x42 |
| 2 |
k1=-k综上可知,存在常数λ=-1. …(15分)
点评:本题考查的知识点是直线与圆锥曲线的关系,椭圆的标准方程,联立方程+韦达定理+设而不求,是解答此类问题的关键方法,但本题运算量巨大,属于难题.

练习册系列答案
相关题目