题目内容
 如图,已知直线l:x=my+1过椭圆C:
如图,已知直线l:x=my+1过椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且
| MA |
| AF |
| MB |
| BF |
(Ⅲ)连接AE、BD,试证明当m变化时,直线AE与BD相交于定点N(
| 5 |
| 2 |
分析:(Ⅰ)由题设条件能够求出c=1,b=
,从而求出椭圆C的方程.
(Ⅱ)设直线l交椭圆于A(x1,y1),B(x2,y2),联立方程组,由根与系数的关系推导λ1+λ2的值.
(Ⅲ)由题设条件想办法证明点N(
,0)在既直线lAE上,又在直线lBD上,∴当m变化时,AE与BD相交于定点(
,0).
| 3 |
(Ⅱ)设直线l交椭圆于A(x1,y1),B(x2,y2),联立方程组,由根与系数的关系推导λ1+λ2的值.
(Ⅲ)由题设条件想办法证明点N(
| 5 |
| 2 |
| 5 |
| 2 |
解答:解:(Ⅰ)易知椭圆右焦点F(1,0),∴c=1,
抛物线x2=4
y的焦点坐标(0,
),∴b=
∴b2=3
∴a2=b2+c2=4∴椭圆C的方程
+
=1
(Ⅱ)易知m≠0,且l与y轴交于M(0,-
),
设直线l交椭圆于A(x1,y1),B(x2,y2)
由
?(3m2+4)y2+6my-9=0
∴△=(6m)2+36(3m2+4)=144(m2+1)>0
∴y1+y2=-
,y1•y2=-
又由
=λ1
∴(x1,y1+
)=λ1(1-x1,-y1)
∴λ1=-1-
同理λ2=-1-
∴λ1+λ2=-2-
(
+
)
∵
+
=
=-
•(-
)=
∴λ1+λ2=-2-
(
+
)=-2-
•
=-
所以,当m变化时,λ1+λ2的值为定值-
;
(Ⅲ)证明:由(Ⅱ)知A(x1,y1),B(x2,y2),∴D(4,y1),E(4,y2)
方法1)∵lAE:y-y2=
•(x-4)
当x=
时,y=y2+
•(-
)=
=
=
=
=0
∴点N(
,0)在直线lAE上,
同理可证,点N(
,0)也在直线lBD上;
∴当m变化时,AE与BD相交于定点(
,0)
方法2)∵kEN=
=
kAN=
=
=
kEN-kAN=
-
=
=
=
=0
∴kEN=kAN∴A、N、E三点共线,
同理可得B、N、D也三点共线;
∴当m变化时,AE与BD相交于定点(
,0).
抛物线x2=4
| 3 |
| 3 |
| 3 |
∴a2=b2+c2=4∴椭圆C的方程
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)易知m≠0,且l与y轴交于M(0,-
| 1 |
| m |
设直线l交椭圆于A(x1,y1),B(x2,y2)
由
|
∴△=(6m)2+36(3m2+4)=144(m2+1)>0
∴y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
又由
| MA |
| AF |
| 1 |
| m |
∴λ1=-1-
| 1 |
| my1 |
同理λ2=-1-
| 1 |
| my2 |
∴λ1+λ2=-2-
| 1 |
| m |
| 1 |
| y1 |
| 1 |
| y2 |
∵
| 1 |
| y1 |
| 1 |
| y2 |
| y1+y2 |
| y1y2 |
| 6m |
| 3m2+4 |
| 3m2+4 |
| 9 |
| 2m |
| 3 |
∴λ1+λ2=-2-
| 1 |
| m |
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| m |
| 2m |
| 3 |
| 8 |
| 3 |
所以,当m变化时,λ1+λ2的值为定值-
| 8 |
| 3 |
(Ⅲ)证明:由(Ⅱ)知A(x1,y1),B(x2,y2),∴D(4,y1),E(4,y2)
方法1)∵lAE:y-y2=
| y2-y1 |
| 4-x1 |
当x=
| 5 |
| 2 |
| y2-y1 |
| 4-x1 |
| 3 |
| 2 |
| 2(4-x1)•y2-3(y2-y1) |
| 2(4-x1) |
| 2(4-my1-1)•y2-3(y2-y1) |
| 2(4-x1) |
| 3(y2+y1)-2my1y2 |
| 2(4-x1) |
=
3×
| ||||
| 2(4-x1) |
∴点N(
| 5 |
| 2 |
同理可证,点N(
| 5 |
| 2 |
∴当m变化时,AE与BD相交于定点(
| 5 |
| 2 |
方法2)∵kEN=
| y2 | ||
4-
|
| 2y2 |
| 3 |
| y1 | ||
x1-
|
| y1 | ||
my1+1-
|
| 2y1 |
| 2my1-3 |
| 2y2 |
| 3 |
| 2y1 |
| 2my1-3 |
| 2y2(2my1-3)-6y1 |
| 3(2my1-3) |
=
| 4my1y2-6(y1+y2) |
| 3(2my1-3) |
4m×
| ||||
| 3(2my1-3) |
∴kEN=kAN∴A、N、E三点共线,
同理可得B、N、D也三点共线;
∴当m变化时,AE与BD相交于定点(
| 5 |
| 2 |
点评:本题是椭圆的综合应用题,有一定的难度.解题时要认真审题,注意挖掘隐含条件,仔细作答.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2. 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: (2012•乐山二模)如图,已知直线L:x=my+1过椭圆C:
(2012•乐山二模)如图,已知直线L:x=my+1过椭圆C: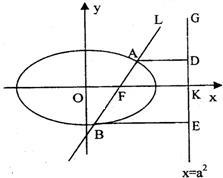 如图,已知直线L:
如图,已知直线L: