题目内容
已知:定义在区间[- ,π]上的函数y=f(x)的图像关于直线x=
,π]上的函数y=f(x)的图像关于直线x= 对称,当x≥
对称,当x≥ 时,函数f(x)=sinx.
时,函数f(x)=sinx.
(1)求f(- ),f(-
),f(- )的值;
)的值;
(2)求y=f(x)的函数表达式(直接写表达式只得2分);
(3)如果关于x的方程f(x)=a有解,那么将方程在a取某一确定值时所求得的所有解的和记为Ma.求Ma的所有可能取值及相对应的a的取值范围.
答案:
解析:
解析:
|
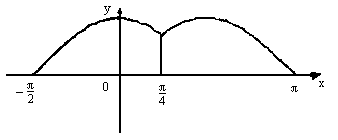
[解](1)f(- f(- (2)当- f(x)= (3)作函数f(x)的图像
显然,若f(x)=a有解,则a∈[0,1] ①0≤a< ②a= ③ ④a=1,f(x)=a有两解,Ma= |

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
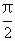 )=f(π)=sinπ=0
)=f(π)=sinπ=0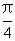 )=f(
)=f(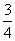 π)=
π)=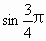 =
=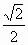
 =cosx
=cosx
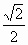 ,f(x)=a有两解,Ma=
,f(x)=a有两解,Ma=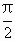 .
. π.
π. (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件该产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件该产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金). ,过焦点F且斜率为
,过焦点F且斜率为 如图,圆
如图,圆 与圆
与圆 内切于点
内切于点 ,其半径分别为
,其半径分别为 与
与 ,
, 交圆
交圆 (
( 为定值。
为定值。 ,向量
,向量 ,求向量
,求向量 ,使得
,使得 .
. 中,求过椭圆
中,求过椭圆 (
( 为参数)的右焦点且与直线
为参数)的右焦点且与直线 (
( 为参数)平行的直线的普通方程。
为参数)平行的直线的普通方程。