题目内容
9.已知集合S={1,2,…,1997},A={a1,a2,…,an}是S的子集,且具有下列性质:“A中任意两个不同元素的和不能被117整除.”试确定A中元素个数的最大值并证明你的结论.
分析 集合{1,2,3,…,1997}中所有的数都除以117取余数,可分为117组,即余数分别为0,1,2,…,116,余数和为117的不能同时出现在A中,进而分析可得答案.
解答 解:集合{1,2,3,…,1997}中所有的数都除以117取余数,可分为117组,即余数分别为0,1,2,…,116;
其中余数为0时,有{117,234,351,…,1989}共17个,
余数为1时,有{1,118,235,…,1990}共18个;
余数为2时,有{2,119,236,…,1991}共18个;
…
余数为8时,有{8,125,242,…,1997}共18个;
余数为9时,有{9,126,243,…,1881}共17个;
余数为10时,有{10,127,244,…,1882}共17个;
…
余数为116时,有{116,233,350,…,1988}共17个;
根据题意知,余数为1和余数为116,余数为2和余数为115,…,余数为58和余数为59不能同时在A中,余数为0时只能有一个元素在A中;
所以,A最大时应是余数为1时+余数为2时+…+余数为8时+余数为9(或余数为108)时+余数为10(或余数为107)时+…+余数为58(或余数为59)时+余数为0时的一个元素,
共995个元素.
即A的元素最多为995个.
点评 本题考查的知识点是元素与集合关系的判断,分类讨论思想,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列函数中值域是R+的是( )
| A. | y=$\sqrt{{x}^{2}-3x+10}$ | B. | y=2x+1(x>0) | C. | y=$\frac{1}{{x}^{2}}$ | D. | y=2x(x>0) |
14.已知全集为R,集合A={x|x≤1},B={x|x≥-2},则A∪B=( )
| A. | R | B. | {x|-2≤x≤1} | C. | A | D. | B |
18.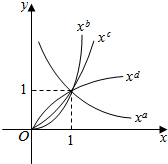 幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )
幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )
 幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )
幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )| A. | a>b>c>d | B. | d>b>c>a | C. | d>c>b>a | D. | b>c>d>a |