题目内容
已知函数![]() 满足:①
满足:①![]() ;②
;②![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,是否存在实数
,是否存在实数![]() 使
使![]() 为偶函数;若存在,求出
为偶函数;若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(平行班做)(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(特保班做)(3)设函数![]() ,讨论此函数在定义域范围内的零点个数.
,讨论此函数在定义域范围内的零点个数.
解:(1)![]() ,
,![]() ①
①
又![]() ,即
,即![]() ,②
,②
将①式代入②式,得![]() ,又∵
,又∵![]() ,
,
∴![]() ,
,![]() . ……………………………………………4分
. ……………………………………………4分
(2)由(1)得![]() ,
,
![]() ,
,
假设存在实数![]() 使
使![]() 为偶函数,则有
为偶函数,则有
![]() ,即
,即![]() ,可得
,可得![]() .
.
故存在实数![]() 使
使![]() 为偶函数.……………………………………8分
为偶函数.……………………………………8分
平行班(3)依题意有![]() ,
,
![]() 在区间
在区间![]() 上单调递增,
上单调递增,
若函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则
![]() 且
且![]() 在区间
在区间![]() 上恒成立,
上恒成立,
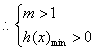 ,即
,即![]() 解得
解得![]() ;
;
故实数![]() 的取值范围是
的取值范围是![]() .……………………………………12分
.……………………………………12分
特保班(3)方法1 ∵ 函数![]() ,
,
![]()
![]() 有解,即
有解,即![]()
又∵ ![]() ,
,
∴ ![]() 的最小值为
的最小值为![]() ,
,
∴ ![]() ;
;
又![]()
![]() ,
,
即![]() , (*)
, (*)
![]()
∴当![]() 时,方程(*)有2个不同的实数根;
时,方程(*)有2个不同的实数根;
当![]() 时,方程(*)有1个实数根;
时,方程(*)有1个实数根;
当![]() 时,方程(*)没有实数根.
时,方程(*)没有实数根.
综上,当![]() 时,函数
时,函数![]() 在定义域范围内有2个零点;
在定义域范围内有2个零点;
当![]() 时,函数
时,函数![]() 在定义域范围内有1个零点;
在定义域范围内有1个零点;
当![]() 时,函数
时,函数![]() 在定义域范围内没有零点.…………12分
在定义域范围内没有零点.…………12分
方法2∵ 函数![]() ,
,
![]()
![]() 有解,
有解,![]()
又∵ ![]() ,
,
∴ ![]() 的最小值为
的最小值为![]() ,
,
∴ ![]() ;
;
又![]()
![]() ,
,
即![]()
![]()
∴当![]() 时,直线
时,直线![]() 与抛物线
与抛物线![]() 有2个不同的交点;
有2个不同的交点;
当![]() 时,直线
时,直线![]() 与抛物线
与抛物线![]() 有1个交点;
有1个交点;
当![]() 时,直线
时,直线![]() 与抛物线
与抛物线![]() 没有交点.
没有交点.
综上,当![]() 时,函数
时,函数![]() 在定义域范围内有2个零点;
在定义域范围内有2个零点;
![]() 当
当![]() 时,函数
时,函数![]() 在定义域范围内有1个零点;
在定义域范围内有1个零点;
当![]() 时,函数
时,函数![]() 在定义域范围内没有零点.…
在定义域范围内没有零点.…
