题目内容
已知函数f(x)定义域为[0,1],且同时满足
(1)对于任意x∈[0,1],且同时满足;
(2)f(1)=4;
(3)若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.
(Ⅰ)试求f(0)的值;
(Ⅱ)试求函数f(x)的最大值;
(Ⅲ)设数列{an}的前n项和为Sn,满足a1=1,Sn=![]() (an-3),n∈N*.
(an-3),n∈N*.
求证:f(a1)+f(a2)+…+f(an)<![]() log3
log3![]() .
.
解析:
|
解答:(Ⅰ)令x1=x2=0,则有f(0)≥2f(0)-3,即f(0)≤3. 又对任意x∈[0,1],总有f(x)≥3,所以f(0)=3. (Ⅱ)任取x1,x2∈[0,1],x1<x2, f(x2)=f[x1+(x2-x1)]≥f(x1)+f(x2-x1)-3. 因为0<x2-x1≤1,∴f(x2-x1)≥3. ∴f(x2)≥f(x1)+3-3=f(x1). ∴当x∈[0,1]时,f(x)≤f(1)=4,所以函数f(x)的最大值为4. (Ⅲ)当n>1时,an=Sn―Sn-1= ∴数列{an}是以a1=1为首项,公比为 an=1×( f(1)=f[3n-1· 4≥3n-1f( ∴f( ∴f(a1)+f(a2)+…+f(an)≤(3+ =3n+ 又 ∴原不等式成立. |
提示:
|
分析:(Ⅰ)令x=y=0赋值法和不等号的性质求f(0)的值;(Ⅱ)证明函数f(x)在[0,1]上的单调性求f(x)的最大值;(Ⅲ)先根据条件求数列{an}的通项公式,利用条件f(x1+x2)≥f(x1)+f(x2)-3放大f( 说明:这是一道涉及函数的单调性的应用、不等式的证明、数列的通项与求和的综合性题,难度较大,对思维能力要求较高,要求具有熟练掌握函数单调性的证明方法、数列求和和放缩法证明不等式等推理能力. |

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案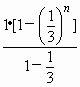 =3n+
=3n+