题目内容
(本小题满分12分)
在直角坐标系中,已知 ,
, ,
, 为坐标原点,
为坐标原点, ,
, .
.
(Ⅰ)求 的对称中心的坐标及其在区间
的对称中心的坐标及其在区间 上的单调递减区间;
上的单调递减区间;
(Ⅱ)若 ,
, ,求
,求 的值。
的值。
在直角坐标系中,已知
 ,
, ,
, 为坐标原点,
为坐标原点, ,
, .
.(Ⅰ)求
 的对称中心的坐标及其在区间
的对称中心的坐标及其在区间 上的单调递减区间;
上的单调递减区间;(Ⅱ)若
 ,
, ,求
,求 的值。
的值。(Ⅰ)对称中心是
 的单调递减是
的单调递减是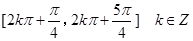 ,
,
 在区间
在区间 上的单调递减区间为
上的单调递减区间为 .
.
(Ⅱ) 。
。

 的单调递减是
的单调递减是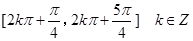 ,
, 在区间
在区间 上的单调递减区间为
上的单调递减区间为 .
.(Ⅱ)
 。
。本试题主要是考查了三角函数的性质和图像的综合运用。
(1)利用向量的数量积公式,得到三角函数关系式,然后得到函数的对称中心和单调区间的求解。
(2)
 ,
, ,得到三角方程的解。
,得到三角方程的解。
解: ,
, ,
,
则
 ………………2分
………………2分




 ………………………4分
………………………4分
(Ⅰ)由 ,即
,即
 对称中心是
对称中心是
当 时
时 单调递减,即
单调递减,即

 的单调递减是
的单调递减是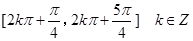 …………………6分
…………………6分
 在区间
在区间 上的单调递减区间为
上的单调递减区间为 .……………8分
.……………8分
(Ⅱ)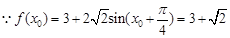

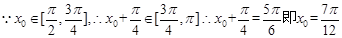 ………………10分
………………10分
 。………………12分
。………………12分
(1)利用向量的数量积公式,得到三角函数关系式,然后得到函数的对称中心和单调区间的求解。
(2)

 ,
, ,得到三角方程的解。
,得到三角方程的解。解:
 ,
, ,
,则

 ………………2分
………………2分



 ………………………4分
………………………4分(Ⅰ)由
 ,即
,即
 对称中心是
对称中心是
当
 时
时 单调递减,即
单调递减,即

 的单调递减是
的单调递减是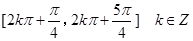 …………………6分
…………………6分 在区间
在区间 上的单调递减区间为
上的单调递减区间为 .……………8分
.……………8分(Ⅱ)
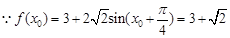

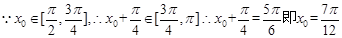 ………………10分
………………10分 。………………12分
。………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
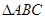 中,角
中,角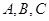 所对的三边分别为
所对的三边分别为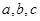 成等比数列,且
成等比数列,且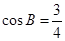 .
.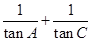 的值;
的值; 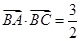 ,求
,求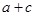 的值.
的值. 的图像向右平移
的图像向右平移 个单位长度,所得图像经过点
个单位长度,所得图像经过点 则
则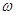 的最小值是( )
的最小值是( )

 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 ,若
,若 ,且
,且 .
. 的值; (2)若
的值; (2)若 ,求△
,求△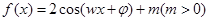 ,对任意实数
,对任意实数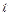 都有
都有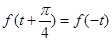 ,且
,且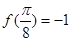 ,则实数
,则实数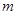 的值等于
的值等于  ;
;
 ,
, 为偶函数时,求
为偶函数时,求 的值。
的值。 时,
时, 在
在 上是单调递增函数,求
上是单调递增函数,求 的取值范围。
的取值范围。 时,(其中
时,(其中 ,
, ),若
),若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。 ( )
( )



 ,那么tan x等于( )
,那么tan x等于( )



 的图象,这五个点可以分别是
的图象,这五个点可以分别是 ,
, ,
, , ,
, ,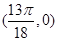 .
.