题目内容
已知P为抛物线y2=4(x-1)上动点,PA⊥y轴交y于A,点B在y轴上,且B点分向量
的比为1:2,求BP中点的轨迹方程.
| OA |
分析:设P(t2+1,2t),由条件可得B(0,
t),BP中点M(x,y),则
,消去参数t化为普通方程,即为所求.
| 2 |
| 3 |
|
解答: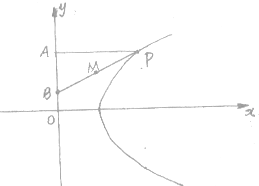 解:设P(t2+1,2t),(t∈R),则A(0,2t),
解:设P(t2+1,2t),(t∈R),则A(0,2t),
∵
=1:2,
∴B(0,
t).
设BP中点M(x,y),则
,消去参数t化为 9y2-32x+16=0,
故BP中点的轨迹方程为 9y2-32x+16=0.
 解:设P(t2+1,2t),(t∈R),则A(0,2t),
解:设P(t2+1,2t),(t∈R),则A(0,2t),∵
| OB |
| BA |
∴B(0,
| 2 |
| 3 |
设BP中点M(x,y),则
|
故BP中点的轨迹方程为 9y2-32x+16=0.
点评:本题主要考查抛物线的标准方程,以及简单性质的应用,求曲线的参数方程,以及把参数方程化为普通方程的方法,属于中档题.

练习册系列答案
相关题目
已知P为抛物线y2=4x上一个动点,Q为圆x2+(y-4)2=1上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是( )
A、2
| ||
B、2
| ||
C、
| ||
D、
|