Question

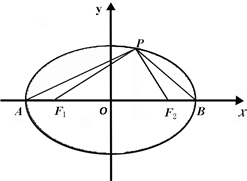（2007•广州模拟）如图，已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

4

5

，左、右焦点分别为F₁和F₂，椭圆C与x轴的两交点分别为A、B，点P是椭圆上一点（不与点A、B重合），且∠APB=2α，∠F₁PF₂=2β．
（Ⅰ）若β=45°，三角形F₁PF₂的面积为36，求椭圆C的方程；
（Ⅱ）当点P在椭圆C上运动，试证明tanβ•tan2α为定值．

Answer 1

分析：（Ⅰ）由题意三角形F₁PF₂为直角三角形，所以|PF1|2+|PF2|2=|F1F2|2，即(|PF1|+|PF2|)2-2|PF1||PF2|=|F1F2|2，结合三角形F₁PF₂的面积为36，可求得b²=36，利用椭圆C的离心率为

4

5

，可得a²=100，从而可求椭圆C的方程；
（Ⅱ）不妨设点P（x，y）在第一象限，则在三角形PF₁F₂中，|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos2β，从而可得4c²=4a²-2|PF₁||PF₂|（1+cos2β），进而有S△F1F2P=

1

2

|PF1||PF2|sin2β=

b2sin2β

2cos2β

=

b2sinβ

cosβ

=b2tanβ．
由S△F1F2P=

1

2

×2c×y=cy，可得tanβ=

cy

b2

．作PC⊥x轴，垂足为C，故可求得tan2α=

2ay

x2+y2-a2

=

2a

(1- a2 b2 )y

=

2ab2

-c2y

，进而得tanβ•tan2α=

2

- c a

=

2

-e

，利用离心率e=

4

5

，可求tanβ•tan2α是定值．

解答：解：（Ⅰ）∵∠F₁PF₂=2β=90°
∴三角形F₁PF₂为直角三角形，
∴|PF1|2+|PF2|2=|F1F2|2，
∴(|PF1|+|PF2|)2-2|PF1||PF2|=|F1F2|2，
∵三角形F₁PF₂的面积为36，
∴

1

2

|PF1||PF2|=36，
∴|PF₁||PF₂|=72
∴（2a）²-2×72=（2c）²，
∴b²=36．                                              …（2分）
∵椭圆C的离心率为

4

5

，则

c2

a2

=

16

25

，即

a2-b2

a2

=

16

25

，
∴a²=100，
∴椭圆C的方程为

x2

100

+

y2

36

=1．                            …（4分）
（Ⅱ）不妨设点P（x，y）在第一象限，则在三角形PF₁F₂中，|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos2β，
∴|F1F2|2=(|PF1|+|PF2|)2-2|PF1||PF2|(1+cos2β)，
即4c²=4a²-2|PF₁||PF₂|（1+cos2β），
∴|PF1||PF2|=

2b2

1+cos2β

=

2b2

2cos2β

=

b2

cos2β

．
∴S△F1F2P=

1

2

|PF1||PF2|sin2β=

b2sin2β

2cos2β

=

b2sinβ

cosβ

=b2tanβ．
∵S△F1F2P=

1

2

×2c×y=cy，
∴b²tanβ=cy，即tanβ=

cy

b2

．                           …（6分）
作PC⊥x轴，垂足为C．
∵tan∠APC=

|AC|

|PC|

=

a+x

y

，tan∠CPB=

|CB|

|PC|

=

a-x

y

，
∴tan2α=tan(∠APC+∠CPB)=

a+x y + a-x y

1- a2-x2 y2

=

2ay

x2+y2-a2

．
∵

x2

a2

+

y2

b2

=1，∴x2=a2-

a2y2

b2

．
∴tan2α=

2ay

x2+y2-a2

=

2a

(1- a2 b2 )y

=

2ab2

-c2y

．                 …（8分）

∴tanβ•tan2α=

2

- c a

=

2

-e

，
∵离心率e=

4

5

，
∴tanβ•tan2α=-

5

2

．
∴tanβ•tan2α是定值，其值为-

5

2

．                           …（10分）

点评：本题以椭圆的性质为载体，考查椭圆的标准方程，考查焦点三角形的面积计算，考查余弦定理的运用，综合性强．