题目内容
关于函数f(x)=lg (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题:①函数y=f(x)的图象关于y轴对称;
②当x>0时,f(x)是增函数,当x<0时,f(x)是减函数;
③函数f(x)的最小值是lg2;
④当-1<x<0或x>1时,f(x)为增函数;
⑤f(x)无最大值,也无最小值.
其中正确命题的序号是
【答案】分析:①判断函数是否为偶函数即可.
②将复合函数转化为两个基本函数,令t=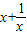 (x>0),易知在(0,1]上是减函数,在[1,+∞)上是增函数.
(x>0),易知在(0,1]上是减函数,在[1,+∞)上是增函数.
③因为t=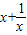 ≥2(x>0),再由偶函数,可知正确.
≥2(x>0),再由偶函数,可知正确.
④当-1<x<0或x>1时函数t=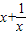 是增函数,再根据复合函数判断.
是增函数,再根据复合函数判断.
⑤用③来判断.
解答:解:①定义域为R,又满足f(-x)=f(x),所以函数y=f(x)的图象关于y轴对称,正确.
②令t= (x>0),在(0,1]上是减函数,在[1,+∞)上是增函数,不正确.
(x>0),在(0,1]上是减函数,在[1,+∞)上是增函数,不正确.
③t=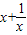 ≥2,又是偶函数,所以函数f(x)的最小值是lg2,正确.
≥2,又是偶函数,所以函数f(x)的最小值是lg2,正确.
④当-1<x<0或x>1时函数t=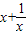 是增函数,根据复合函数知,f(x)是增函数,正确.
是增函数,根据复合函数知,f(x)是增函数,正确.
⑤由③知,不正确.
故答案为:①③④
点评:本题通过多个问题来考查函数复合函数的研究方法,涉及了函数的奇偶性,单调性,最值等,知识点,方法灵活,要细心耐心.
②将复合函数转化为两个基本函数,令t=
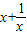 (x>0),易知在(0,1]上是减函数,在[1,+∞)上是增函数.
(x>0),易知在(0,1]上是减函数,在[1,+∞)上是增函数.③因为t=
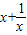 ≥2(x>0),再由偶函数,可知正确.
≥2(x>0),再由偶函数,可知正确.④当-1<x<0或x>1时函数t=
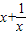 是增函数,再根据复合函数判断.
是增函数,再根据复合函数判断.⑤用③来判断.
解答:解:①定义域为R,又满足f(-x)=f(x),所以函数y=f(x)的图象关于y轴对称,正确.
②令t=
 (x>0),在(0,1]上是减函数,在[1,+∞)上是增函数,不正确.
(x>0),在(0,1]上是减函数,在[1,+∞)上是增函数,不正确.③t=
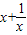 ≥2,又是偶函数,所以函数f(x)的最小值是lg2,正确.
≥2,又是偶函数,所以函数f(x)的最小值是lg2,正确.④当-1<x<0或x>1时函数t=
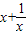 是增函数,根据复合函数知,f(x)是增函数,正确.
是增函数,根据复合函数知,f(x)是增函数,正确.⑤由③知,不正确.
故答案为:①③④
点评:本题通过多个问题来考查函数复合函数的研究方法,涉及了函数的奇偶性,单调性,最值等,知识点,方法灵活,要细心耐心.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知函数f(x)=sin(2x-
)的图象为L,下列说法不正确的是( )
| π |
| 6 |
A、图象L关于直线x=
| ||||
B、图象L关于点(
| ||||
C、函数f(x)在(-
| ||||
D、将L先向左平移
|