题目内容
已知向量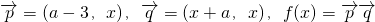 ,且m,n是方程f(x)=0的两个实根,
,且m,n是方程f(x)=0的两个实根,
(1)设g(a)=m3+n3+a3,求g(a)的最小值;
(2)若不等式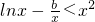 在x∈[1,+∞)上恒成立,求实数b的取值范围;
在x∈[1,+∞)上恒成立,求实数b的取值范围;
(3)对于(1)中的函数y=g(a),给定函数h(x)=c(xlnx-x3),(c<0),若对任意的x0∈[2,3],总存在x1∈[1,2],使得g(x0)=h(x1),求实数c的取值范围.
解:(1)f(x)=x2+(a-3)x+a2-3a有两个实根,
所以△≥0,解得a∈[-1,3]
由题意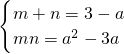
g(a)=m3+n3+a3=(m+n)[(m+n)2-3mn]+a3=3a3-9a2+27,a∈[-1,3]
g′(a)=9a(a-2)=0,解得a=0或2
g(0)=g(3)=27,g(-1)=g(2)=15
所以最小值为15.
(2)若不等式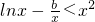 在
在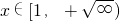 上恒成立,即
上恒成立,即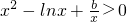 恒成立,
恒成立,
解得b>x(lnx-x2)
令h(x)=x(lnx-x2),x∈[1,+∞)
则h'(x)=1+lnx-3x2,x∈[1,+∞)
则h′′(x)= -6x,x∈[1,+∞)
-6x,x∈[1,+∞)
∵h′′(x)= -6x<0在[1,+∞)恒成立
-6x<0在[1,+∞)恒成立
∴h'(x)=1+lnx-3x2,在区间[1,+∞)为减函数
则h'(x)≤h'(1)=-2<0恒成立
∴h(x)=x(lnx-x2)在区间[1,+∞)递减
则h(x)≤h(1)=-1
故b>-1
(3)由(1)得对任意的x0∈[2,3],g(x0)∈[15,27]
由(2)得函数h(x)=c(xlnx-x3),(c<0),在区间[1,2]单调递增
则h(1)=-c≤h(x)≤h(2)=c(2ln2-8)
若对任意的x0∈[2,3],总存在x1∈[1,2],使得g(x0)=h(x1),
则-c≤15且c(2ln2-8)≥27
解得:-15≤c≤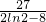
分析:(1)根据f(x)=x2+(a-3)x+a2-3a有两个实根,得到△≥0,解得a∈[-1,3],又由题意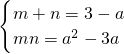 从而g(a)=m3+n3+a3=(m+n)[(m+n)2-3mn]+a3=3a3-9a2+27,a∈[-1,3]利用导数即可求得最小值为15.
从而g(a)=m3+n3+a3=(m+n)[(m+n)2-3mn]+a3=3a3-9a2+27,a∈[-1,3]利用导数即可求得最小值为15.
(2)先将不等式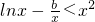 在
在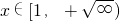 上恒成立,转化为
上恒成立,转化为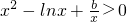 恒成立,即b>x(lnx-x2),构造令h(x)=x(lnx-x2),x∈[1,+∞)可得h'(x)=1+lnx-3x2,h′′(x)=
恒成立,即b>x(lnx-x2),构造令h(x)=x(lnx-x2),x∈[1,+∞)可得h'(x)=1+lnx-3x2,h′′(x)= -6x,根据导函数符号与函数单调性的关系,及判断出函数h(x)的单调性,进而得到答案.
-6x,根据导函数符号与函数单调性的关系,及判断出函数h(x)的单调性,进而得到答案.
(3)由(1)和(2)的结论,我们易求出函数y=g(a)在区间[2,3]上的值域,及函数h(x)=c(xlnx-x3)在[1,2]的上的值域,再结合对任意的x0∈[2,3],总存在x1∈[1,2],使得g(x0)=h(x1),构造关于c的不等式组,解不等式组即可得到答案.
点评:本小题主要考查函数恒成立问题、利用导数求闭区间上函数的最值、不等式的解法等基础知识,考查运算求解能力,转化思想.属于中档题.
所以△≥0,解得a∈[-1,3]
由题意
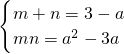
g(a)=m3+n3+a3=(m+n)[(m+n)2-3mn]+a3=3a3-9a2+27,a∈[-1,3]
g′(a)=9a(a-2)=0,解得a=0或2
g(0)=g(3)=27,g(-1)=g(2)=15
所以最小值为15.
(2)若不等式
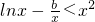 在
在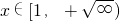 上恒成立,即
上恒成立,即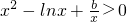 恒成立,
恒成立,解得b>x(lnx-x2)
令h(x)=x(lnx-x2),x∈[1,+∞)
则h'(x)=1+lnx-3x2,x∈[1,+∞)
则h′′(x)=
 -6x,x∈[1,+∞)
-6x,x∈[1,+∞)∵h′′(x)=
 -6x<0在[1,+∞)恒成立
-6x<0在[1,+∞)恒成立∴h'(x)=1+lnx-3x2,在区间[1,+∞)为减函数
则h'(x)≤h'(1)=-2<0恒成立
∴h(x)=x(lnx-x2)在区间[1,+∞)递减
则h(x)≤h(1)=-1
故b>-1
(3)由(1)得对任意的x0∈[2,3],g(x0)∈[15,27]
由(2)得函数h(x)=c(xlnx-x3),(c<0),在区间[1,2]单调递增
则h(1)=-c≤h(x)≤h(2)=c(2ln2-8)
若对任意的x0∈[2,3],总存在x1∈[1,2],使得g(x0)=h(x1),
则-c≤15且c(2ln2-8)≥27
解得:-15≤c≤
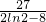
分析:(1)根据f(x)=x2+(a-3)x+a2-3a有两个实根,得到△≥0,解得a∈[-1,3],又由题意
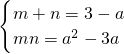 从而g(a)=m3+n3+a3=(m+n)[(m+n)2-3mn]+a3=3a3-9a2+27,a∈[-1,3]利用导数即可求得最小值为15.
从而g(a)=m3+n3+a3=(m+n)[(m+n)2-3mn]+a3=3a3-9a2+27,a∈[-1,3]利用导数即可求得最小值为15.(2)先将不等式
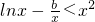 在
在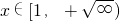 上恒成立,转化为
上恒成立,转化为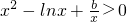 恒成立,即b>x(lnx-x2),构造令h(x)=x(lnx-x2),x∈[1,+∞)可得h'(x)=1+lnx-3x2,h′′(x)=
恒成立,即b>x(lnx-x2),构造令h(x)=x(lnx-x2),x∈[1,+∞)可得h'(x)=1+lnx-3x2,h′′(x)= -6x,根据导函数符号与函数单调性的关系,及判断出函数h(x)的单调性,进而得到答案.
-6x,根据导函数符号与函数单调性的关系,及判断出函数h(x)的单调性,进而得到答案.(3)由(1)和(2)的结论,我们易求出函数y=g(a)在区间[2,3]上的值域,及函数h(x)=c(xlnx-x3)在[1,2]的上的值域,再结合对任意的x0∈[2,3],总存在x1∈[1,2],使得g(x0)=h(x1),构造关于c的不等式组,解不等式组即可得到答案.
点评:本小题主要考查函数恒成立问题、利用导数求闭区间上函数的最值、不等式的解法等基础知识,考查运算求解能力,转化思想.属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目