题目内容
从一工厂全体工人随机抽取5人，其工龄与每天加工A中零件个数的数据如表：| 工人编号 | 1 | 2 | 3 | 4 | 5 |
| 工龄x（年） | 3 | 5 | 6 | 7 | 9 |
| 个数y（个） | 3 | 4 | 5 | 6 | 7 |
（2）如果y与x线性相关关系，求回归直线方程；
（3）若某名工人的工龄为16年，试估计他每天加工的A种零件个数．
分析：（1）根据所给的数据作出横标和纵标的平均数，得到这组数据的样本中心点，利用最小二乘法作出相关系数，即可得出结论；
（2）利用最小二乘法作出线性回归方程的系数，进而求出a的值，写出线性回归方程．
（3）由回归方程可预报其每天加工的A种零件个数为
=0.7×16+0.8，即工人的工龄为11年，从而估计他每天加工的A种零件个数．
（2）利用最小二乘法作出线性回归方程的系数，进而求出a的值，写出线性回归方程．
（3）由回归方程可预报其每天加工的A种零件个数为
 |
| y |
解答：解：（1）依题意得
═6，
=5，Sx=2，Sy=
，Sxy=2.8，
rxy=
=0.989＞0.8，
∴x与y高度线性相关；
（2）b=
=
=0.7，
a=
-b
=5-6×0.7=0.8，
∴回归方程为：y=0.7x+0.8；
故工人的工龄为11年，试估他每天加工的A种零件个数为12．
. |
| x |
. |
| y |
| 2 |
rxy=
| Sxy |
| Sx•Sy |
∴x与y高度线性相关；
（2）b=
| Sxy |
| Sx |
| 2.8 |
| 4 |
a=
. |
| y |
. |
| x |
∴回归方程为：y=0.7x+0.8；
|
故工人的工龄为11年，试估他每天加工的A种零件个数为12．
点评：本题考查了两个变量的相关关系的判定及回归方程的求法，利用最小二乘法求回归方程的系数是解答此类问题的关键．
练习册系列答案
相关题目
从一工厂全体工人中随机抽取5人，其工龄与每天加工A种零件个数的数据如下表：
（Ⅰ）求y关于x的线性回归方程；
（Ⅱ）若某名工人的工龄为11年，试估计他每天加工的A种零件个数．
（参考公式：
=
，
=
-
）
| 工人编号 | 1 | 2 | 3 | 4 | 5 |
| 工龄 x（年） | 3 | 5 | 6 | 7 | 9 |
| 个数 y（年） | 2 | 3 | 3 | 4 | 5 |
（Ⅱ）若某名工人的工龄为11年，试估计他每天加工的A种零件个数．
（参考公式：
| ? |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
从一工厂全体工人随机抽取5人，其工龄与每天加工A中零件个数的数据如下表：
注：rxy=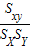
（Sxy=
-
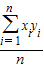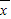
）回归方程：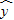
=bx+a，b=
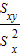，a=
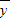-b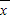
（1）计算x与y的相关关系；
（2）如果y与x的线性相关关系，求回归直线方程
（3）若某名工人的工龄为11年，试估计他每天加工的A种零件个数．
| 工人编号 | 1 | 2 | 3 | 4 | 5 |
| 工龄x（年） | 3 | 5 | 6 | 7 | 9 |
| 个数y（个） | 3 | 4 | 5 | 6 | 7 |
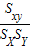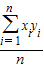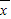
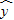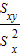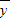（Sxy=-）回归方程：=bx+a，b=，a=-b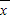（1）计算x与y的相关关系；
（2）如果y与x的线性相关关系，求回归直线方程
（3）若某名工人的工龄为11年，试估计他每天加工的A种零件个数．
从一工厂全体工人中随机抽取5人，其工龄与每天加工A种零件个数的数据如下表：
（Ⅰ）求y关于x的线性回归方程；
（Ⅱ）若某名工人的工龄为11年，试估计他每天加工的A种零件个数．
| 工人编号 | 1 | 2 | 3 | 4 | 5 |
| 工龄 x（年） | 3 | 5 | 6 | 7 | 9 |
| 个数 y（年） | 2 | 3 | 3 | 4 | 5 |
（Ⅱ）若某名工人的工龄为11年，试估计他每天加工的A种零件个数．