题目内容
1、证明两角差的余弦公式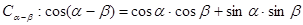 ;
;
2、由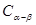 推导两角和的余弦公式
推导两角和的余弦公式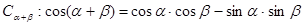 .
.
3、已知△ABC的面积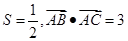 ,且
,且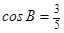 ,求
,求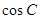 .
.
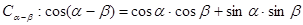 ;
;2、由
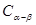 推导两角和的余弦公式
推导两角和的余弦公式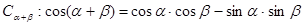 .
.3、已知△ABC的面积
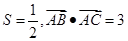 ,且
,且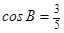 ,求
,求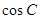 .
.(1)在平面直角坐标系中,以原点为圆心,作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.
设它们的终边分别交单位圆于点P1(cosα,sinα),P2(cosβ,sinβ),即有两单位向量,它们的所成角是|α-β|,根据向量数量积的性质能够证明cos(α-β)=cosαcosβ+sinαsinβ.
(2)先由诱导公式得sin(α+β)=cos( ),再进一步整理为cos[(
),再进一步整理为cos[( )-β],然后利用和差公式和诱导公式能够得到sin(α+β)=sinαcosβ+cosαsinβ
)-β],然后利用和差公式和诱导公式能够得到sin(α+β)=sinαcosβ+cosαsinβ
2、
由 ,
,

由 ,所以
,所以
设它们的终边分别交单位圆于点P1(cosα,sinα),P2(cosβ,sinβ),即有两单位向量,它们的所成角是|α-β|,根据向量数量积的性质能够证明cos(α-β)=cosαcosβ+sinαsinβ.
(2)先由诱导公式得sin(α+β)=cos(
 ),再进一步整理为cos[(
),再进一步整理为cos[( )-β],然后利用和差公式和诱导公式能够得到sin(α+β)=sinαcosβ+cosαsinβ
)-β],然后利用和差公式和诱导公式能够得到sin(α+β)=sinαcosβ+cosαsinβ 2、

由
 ,
,
由
 ,所以
,所以
本试题主要是考查了利用三角函数总两角和差的三角关系式证明。并能,结合向量的知识进行求解三角形问题的综合运用。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
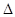 ABC中,
ABC中,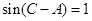 , sinB=
, sinB=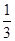 .
.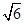 ,求
,求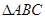 中,
中,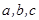 分别是角A、B、C的对边,
分别是角A、B、C的对边,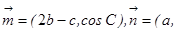
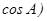 ,且
,且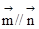 .
.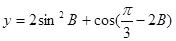 的值域.
的值域. (tan10°+tan20°)= 。
(tan10°+tan20°)= 。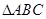 中,角
中,角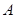 ,
,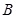 ,
,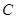 的对边分别为
的对边分别为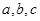 ,且
,且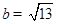 ,
,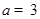 ,求
,求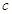 的值;
的值;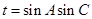 ,求
,求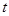 的最大值.
的最大值.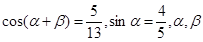 均为锐角,求
均为锐角,求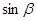 的值。
的值。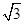 tan24°tan36°=________.
tan24°tan36°=________.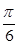 )cosx的最小值是
)cosx的最小值是  ,如
,如 .已知
.已知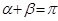 ,
, ,则
,则 ( ).
( ).


