题目内容
设关于x的不等式lg(|x+3|+|x-7|)>a(1)当a=1时,解这个不等式;
(2)当a为何值时,这个不等式的解集为R.
【答案】分析:(1)转化成绝对值不等式,令每项等于零,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集.
(2)解决恒成立问题,可将问题转化为研究函数f(x)的最小值大于a即可.
解答:解:(1)由题意得:|x+3|+|x-7|>10,
当x≥7时x+x-4>10得:x>7(3分)
当-3<x<7时,x+4-x>10不成立(5分)
当x≤-3时-x+4-x>10得:x<-3(7分)
解得:x<-3或x>7(6分)
(2)设t=|x+3|+|x-7|,
则由对数定义及绝对值的几何意义知t≥10,
因y=lgx在(0,+∞)上为增函数,
∵|x+3|+|x-7|的最小值为10,
∴lg(|x+3|+|x-7|)的最小值为1(8分)
要使不等式的解集为R,则须a<1(10分)
点评:本题考查了对数的运算性质,以及绝对值不等式的解法,所谓零点分段法,即令每项等于零,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集.
(2)解决恒成立问题,可将问题转化为研究函数f(x)的最小值大于a即可.
解答:解:(1)由题意得:|x+3|+|x-7|>10,
当x≥7时x+x-4>10得:x>7(3分)
当-3<x<7时,x+4-x>10不成立(5分)
当x≤-3时-x+4-x>10得:x<-3(7分)
解得:x<-3或x>7(6分)
(2)设t=|x+3|+|x-7|,
则由对数定义及绝对值的几何意义知t≥10,
因y=lgx在(0,+∞)上为增函数,
∵|x+3|+|x-7|的最小值为10,
∴lg(|x+3|+|x-7|)的最小值为1(8分)
要使不等式的解集为R,则须a<1(10分)
点评:本题考查了对数的运算性质,以及绝对值不等式的解法,所谓零点分段法,即令每项等于零,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

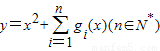 在区间
在区间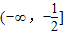 上的最小值为6,求n的值.
上的最小值为6,求n的值.